题目内容
5.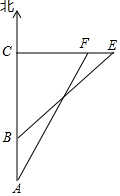 钓鱼岛自古以来就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视检测.如图,E、F为钓鱼岛东西两端.某日,中国一艘海监船从A点向正北方向巡航,其航线距离钓鱼岛最近距离CF=20$\sqrt{3}$海里,在A点测得钓鱼岛最西端F在点A的北偏东30°方向,航线20海里后到达B点,测得最东端E点在B的东北方向(C、F、E在同一直线上).($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{7}$≈2.65,结果精确到0.1)
钓鱼岛自古以来就是中国的领土,中国有关部门已对钓鱼岛及其附属岛屿开展常态化监视检测.如图,E、F为钓鱼岛东西两端.某日,中国一艘海监船从A点向正北方向巡航,其航线距离钓鱼岛最近距离CF=20$\sqrt{3}$海里,在A点测得钓鱼岛最西端F在点A的北偏东30°方向,航线20海里后到达B点,测得最东端E点在B的东北方向(C、F、E在同一直线上).($\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73,$\sqrt{7}$≈2.65,结果精确到0.1)(1)求钓鱼岛东西两端的距离.
(2)若监测船在B点突然检测到F点处有轮艘船出了故障,1.5小时内必须进行抢修.监测船以每小时25海里的速度赶往F点,能否赶到?
分析 (1)首先根据方向角定义结合已知条件,得出∠CAF=30°,FC=20$\sqrt{3}$海里,AB=20海里,∠CBE=45°,然后根据正切函数定义得出AC,再求出EC,进而得出EF长度即可;
(2)连结BF.在Rt△BCF中利用勾股定理得出BF=$\sqrt{B{C}^{2}+C{F}^{2}}$=20$\sqrt{7}$,根据时间=路程÷速度全程监测船所用时间,与1.5小时比较即可.
解答 解:(1)由题意可得出:
∵∠CAF=30°,CF=20$\sqrt{3}$海里,AB=20海里,∠CBE=45°,
∴AC=$\frac{CF}{tan∠CAF}$=$\frac{20\sqrt{3}}{\frac{\sqrt{3}}{3}}$=60(海里),
∴EC=BC=AC-AB=60-20=40(海里),
∴EF=EC-CF=40-20$\sqrt{3}$≈5.4(海里).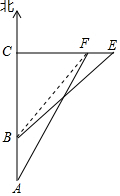 答:钓鱼岛东西两端的距离约为5.4海里.
答:钓鱼岛东西两端的距离约为5.4海里.
(2)如图,连结BF.
在Rt△BCF中,∵∠BCF=90°,
∴BF=$\sqrt{B{C}^{2}+C{F}^{2}}$=$\sqrt{4{0}^{2}+(20\sqrt{3})^{2}}$=20$\sqrt{7}$,
∵监测船以每小时25海里的速度赶往F点,
∴监测船所用时间为:$\frac{20\sqrt{7}}{25}$≈2.12>1.5,
∴监测船以每小时25海里的速度赶往F点,不能赶到.
点评 此题考查了解直角三角形的应用-方向角问题,勾股定理的应用,根据已知得出EC=BC是解(1)题的关键,求出BF的长是解(2)题的关键.

练习册系列答案
相关题目
13.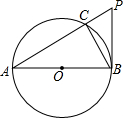 如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PC•PA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
 如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PC•PA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
17.一种药品原价每盒25元,经过两次降价后每盒16元.设两次降价的百分率都为x,则x满足( )
| A. | 16(1+2x)=25 | B. | 25(1-2x)=16 | C. | 16(1+x)2=25 | D. | 25(1-x)2=16 |
14.某单位组织职工开展植树活动,植树量与人数之间关系如图,下列说法不正确的是( )
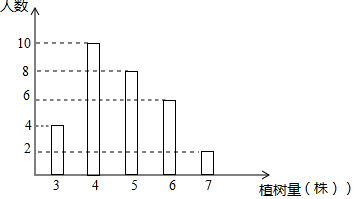

| A. | 参加本次植树活动共有30人 | B. | 每人植树量的众数是4棵 | ||
| C. | 每人植树量的中位数是5棵 | D. | 每人植树量的平均数是5棵 |
15.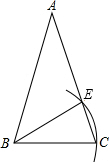 如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
 如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )
如图,已知等腰三角形ABC,AB=AC.若以点B为圆心,BC长为半径画弧,交腰AC于点E,则下列结论一定正确的是( )| A. | AE=EC | B. | AE=BE | C. | ∠EBC=∠BAC | D. | ∠EBC=∠ABE |
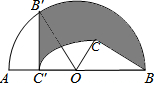 如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为πcm2.
如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为πcm2.