题目内容
2.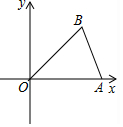 如图,在平面直角坐标系xOy中,已知点A($\sqrt{2}$,0),B(1,1).若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是( )
如图,在平面直角坐标系xOy中,已知点A($\sqrt{2}$,0),B(1,1).若平移点A到点C,使以点O,A,C,B为顶点的四边形是菱形,则正确的平移方法是( )| A. | 向左平移1个单位,再向下平移1个单位 | |
| B. | 向左平移(2$\sqrt{2}$-1)个单位,再向上平移1个单位 | |
| C. | 向右平移$\sqrt{2}$个单位,再向上平移1个单位 | |
| D. | 向右平移1个单位,再向上平移1个单位 |
分析 过点B作BH⊥OA,交OA于点H,利用勾股定理可求出OB的长,进而可得点A向左或向右平移的距离,由菱形的性质可知BC∥OA,所以可得向上或向下平移的距离,问题得解.
解答  解:过B作射线BC∥OA,在BC上截取BC=OA,则四边形OACB是平行四边形,
解:过B作射线BC∥OA,在BC上截取BC=OA,则四边形OACB是平行四边形,
过B作BH⊥x轴于H,
∵B(1,1),
∴OB=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,
∵A($\sqrt{2}$,0),
∴C(1+$\sqrt{2}$,1)
∴OA=OB,
∴则四边形OACB是菱形,
∴平移点A到点C,向右平移1个单位,再向上平移1个单位而得到,
故选D.
点评 本题考查了菱形的性质:菱形具有平行四边形的一切性质;菱形的四条边都相等;菱形的两条对角线互相垂直,并且每一条对角线平分一组对角;

练习册系列答案
相关题目
13.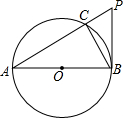 如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PC•PA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
 如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PC•PA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
17.一种药品原价每盒25元,经过两次降价后每盒16元.设两次降价的百分率都为x,则x满足( )
| A. | 16(1+2x)=25 | B. | 25(1-2x)=16 | C. | 16(1+x)2=25 | D. | 25(1-x)2=16 |
14.某单位组织职工开展植树活动,植树量与人数之间关系如图,下列说法不正确的是( )
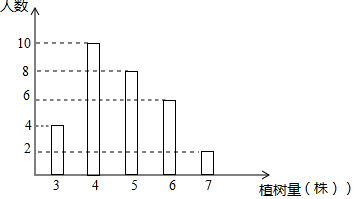

| A. | 参加本次植树活动共有30人 | B. | 每人植树量的众数是4棵 | ||
| C. | 每人植树量的中位数是5棵 | D. | 每人植树量的平均数是5棵 |
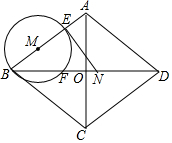 如图,菱形ABCD中,对角线AC,BD相交于点O,AC=12cm,BD=16cm,动点N从点D出发,沿线段DB以2cm/s的速度向点B运动,同时动点M从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随之停止.设运动时间为t(s)(t>0),以点M为圆心,MB长为半径的⊙M与射线BA,线段BD分别交于点E,F,连接EN.
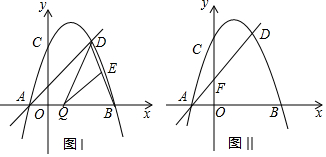
如图,菱形ABCD中,对角线AC,BD相交于点O,AC=12cm,BD=16cm,动点N从点D出发,沿线段DB以2cm/s的速度向点B运动,同时动点M从点B出发,沿线段BA以1cm/s的速度向点A运动,当其中一个动点停止运动时另一个动点也随之停止.设运动时间为t(s)(t>0),以点M为圆心,MB长为半径的⊙M与射线BA,线段BD分别交于点E,F,连接EN.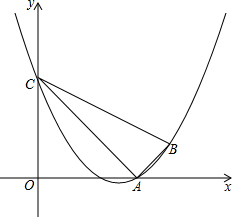 如图,已知二次函数y=ax2+bx+3(a≠0)的图象经过点A(3,0),B(4,1),且与y轴交于点C,连接AB、AC、BC.
如图,已知二次函数y=ax2+bx+3(a≠0)的图象经过点A(3,0),B(4,1),且与y轴交于点C,连接AB、AC、BC.