题目内容
8.我们可以定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.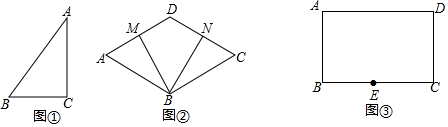
问题探究
(1)如图①已知Rt△ABC中,∠C=90°,AC>BC,试在△ABC内或边上确定一点P,使△BCP为等腰三角形.
(2)如图②,在菱形ABCD中,∠ABC=120°,点M、N分别在AD、CD上,且∠MBN=60°,试判断四边形DMBN是否为“等邻边四边形”?并说明理由.
尝试应用
(3)现有一个矩形材料ABCD,工程人员需要将其制作成一个“等邻边四边形”面板,如图③,在矩形ABCD中,AB=4,BC=6.5,点E在BC上,且BE=3,在矩形ABCD内或者边上,确定一点P,使四边形ABEP为面积最大的“等邻边四边形”,若能实现,请求出最大面积,若不能实现,试说明理由.
分析 (1)如图①中,①以B为圆心,BC为半径画弧交AB于P,此时△PBC是等腰三角形.②以C为圆心,BC为半径画弧交AC于P′,此时△P′BC是等腰三角形.③作线段BC的垂直平分线垂足为F,交AB于E.线段EF上点,都满足条件;
(2)如图②中,结论:四边形DMBN是“等邻边四边形“.只要证明△MBD≌△NBC即可解决问题;
(3)能实现.分两种情形讨论求解即可;
解答 解:(1)如图①中,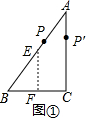
①以B为圆心,BC为半径画弧交AB于P,此时△PBC是等腰三角形.
②以C为圆心,BC为半径画弧交AC于P′,此时△P′BC是等腰三角形.
③作线段BC的垂直平分线垂足为F,交AB于E.线段EF上点,都满足条件.
(2)结论:四边形DMBN是“等邻边四边形“.
理由:如图②中,连接BD.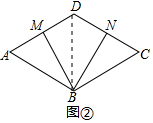
∵四边形ABCD是菱形,∠ABC=120°,
∴∠ABD=∠CBD=60°,AB=BC=CD=AD,
∴△ABD,△BCD都是等边三角形,
∴BD=DC,∠MDB=∠C=60°,
∵∠MBN=∠DBC=60°,
∴∠MBD=∠NBC,
∴△MBD≌△NBC,
∴MB=BN,
∴四边形DMBN是“等邻边四边形“.
(3)能实现.
理由:如图③中,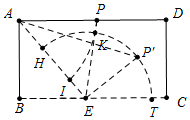
①以A为圆心,AB为半径画弧,当点P在$\widehat{PI}$(不包括点I)上时,四边形ABEP是“等邻边四边形“,点P在AD上时,四边形ABEP的面积的最大值为$\frac{1}{2}$×4×3+$\frac{1}{2}$×4×4=14.
②以E为圆心,EB为半径画弧,当点P在$\widehat{HT}$(不包括点H和点T)上时,四边形ABEP是“等邻边四边形“,P′E⊥AE,AE=5,P′E=3
四边形ABEP的面积的最大值为$\frac{1}{2}$×4×3+$\frac{1}{2}$×5×3=13.5,
综上所述,等邻边四边形ABEP的面积的最大值为14.
点评 本题考查四边形综合题、矩形的性质、菱形的性质、等边三角形的判定和性质、全等三角形的判定和性质、等邻边四边形的定义等知识,解题的关键是理解题意,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.

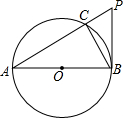 如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.
如图,AB是⊙O的直径,PB与⊙O相切于点B,连接PA交⊙O于点C,连接BC.(1)求证:∠BAC=∠CBP;
(2)求证:PB2=PC•PA;
(3)当AC=6,CP=3时,求sin∠PAB的值.
| A. | 16(1+2x)=25 | B. | 25(1-2x)=16 | C. | 16(1+x)2=25 | D. | 25(1-x)2=16 |
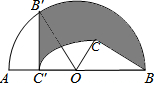 如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为πcm2.
如图,C为半圆内一点,O为圆心,直径AB长为4cm,∠BOC=60°,∠BCO=90°,将△BOC绕圆心O逆时针旋转至△B′OC′,点C′在OA上,则边BC扫过区域(图中阴影部分)的面积为πcm2.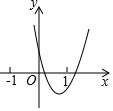 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则正比例函数y=(b+c)x与反比例函数y=$\frac{a-b+c}{x}$在同一坐标系中的大致图象是( )
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,则正比例函数y=(b+c)x与反比例函数y=$\frac{a-b+c}{x}$在同一坐标系中的大致图象是( )


