题目内容
16.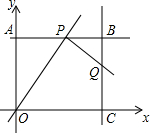 如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q.
如图,在平面直角坐标系中,四边形OABC为矩形,点A、点C分别在y轴、x轴的正半轴上,OA,OC的长分别是方程x2-7x+12=0的两根(OA<OC).P为直线AB上一动点,直线PQ⊥OP交直线BC于点Q.(1)求点B的坐标;
(2)当点P在线段AB上运动(不与A,B重合)时,设点P的横坐标为m,线段CQ的长度为l.求出l关于m的函数解析式;
(3)在坐标平面内是否存在点D,使以O、P、Q、D为顶点的四边形为正方形?若存在,请直接写出D点的坐标;若不存在,请说明理由.
分析 (1)通过解方程求出线段的长度,利用矩形的性质得到AB=4,BC=3,求得B(4,3);
(2)因为点P在线段AB上,点P的横坐标为m,用m表示出AP的长度,利用相似三角形的性质列出比例式求出l关于m的函数解析式;
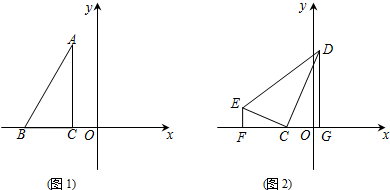
(3)如图,过点D作DE⊥OC于E,由以O、P、Q、D为顶点的四边形为正方形,得到OP=PQ=OD,通过三角形全等,对应边相等求得AP=m=1,再根据另一对三角形全等得到点D的坐标.
解答 解:(1)解方程x2-7x+12=0得:x1=3,x2=4,
∴OA=3,OC=4,
∴A(0,3),C(4,0),
∵四边形OABC为矩形,
∴AB=4,BC=3,
∴B(4,3);
(2)点P在线段AB上,点P的横坐标为m,
∴AP=m,
∵CQ=l,
∴BQ=3-l,
∵∠OAP=∠B=∠OPQ=90°,
∴∠APO+∠BPQ=∠APO+∠AOP=90°,
∴∠APO=∠BPQ,
∴△APO∽△BPQ,
∴$\frac{AP}{BQ}$=$\frac{AO}{PB}$,
即$\frac{m}{3-l}$=$\frac{3}{4-m}$,
∴l=$\frac{1}{3}$m2-$\frac{4}{3}$m+3;
(3)存在,
如图,过点D作DE⊥OC于E,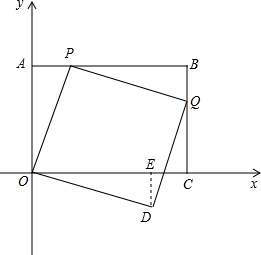
∵四边形ODQP是正方形,
∴OP=PQ=OD,
在△AOP与△BPQ中,
$\left\{\begin{array}{l}{∠AOP=∠BPQ}\\{∠OAP=∠B}\\{PO=PQ}\end{array}\right.$,
∴△AOP≌△BPQ(AAS),
∴PB=OA=3,
∴AP=BP=1,
在△AOP与△OED中,
$\left\{\begin{array}{l}{∠AOP=∠EOD}\\{∠OAP=∠OED}\\{OP=OD}\end{array}\right.$,
∴△AOP≌△OEP(AAS),
∴OE=AO=3,DE=AP=1,
∴D(3,-1).
点评 本题考查了在平面直角坐标系中求点的坐标,相似三角形的判定和性质,全等三角形的判定与性质,特别是(3)正确的画出图形是解题的关键.

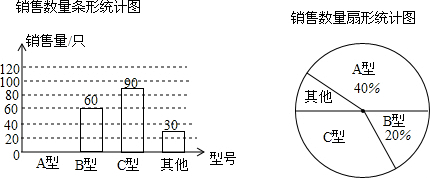
(1)请根据图中提供的信息,将条形图补充完整.
(2)该店4月份只购进了A,B,C三种型号的计算器,其数量和与3份计算器销量的总数量相同,结果恰好用完进化款共8200元,设购进A型计算器x只,B型计算器y只,三种计算器的进价和售价如下表:
| A型 | B型 | C型 | |
| 进价(元/只) | 50 | 30 | 20 |
| 售价(元/只) | 70 | 45 | 25 |
(3)在(2)中的条件下,根据实际情况,预计B型计算器销售超过40只后,这种型号的计算器就会产生滞销.
①假设所购进的A,B,C三种型号计算器能全部售出,求出预估利润P(元)与x(只)的函数关系式;
②求出预估利润的最大值.
| A. | 300° | B. | 240° | C. | 180° | D. | 120° |
 如图,某小区规划在一个长80m、宽50m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,使花草的种植面积共为3800m2.设通道的宽为xm,可依题意列得方程:(80-2x)(50-x)=3800.
如图,某小区规划在一个长80m、宽50m的长方形ABCD上修建三条同样宽的通道,使其中两条与AB平行,另一条与AD平行,其余部分种花草,使花草的种植面积共为3800m2.设通道的宽为xm,可依题意列得方程:(80-2x)(50-x)=3800.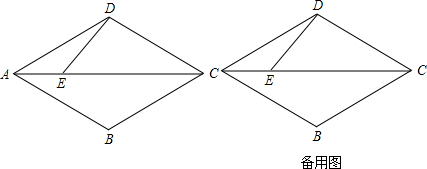
 如图,已知A、D是直线EF上的两点,且∠1+∠2=180°,求证:AB∥CD.
如图,已知A、D是直线EF上的两点,且∠1+∠2=180°,求证:AB∥CD.