题目内容
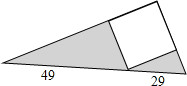 如图所示,空白部分是正方形,求阴影部分的面积.
如图所示,空白部分是正方形,求阴影部分的面积.考点:相似三角形的判定与性质,正方形的性质
专题:
分析:如图,把△ADE绕点D顺时旋转90°,可证明△A′DB为直角三角形,且AD=49,BD=29,可求得其面积.
解答: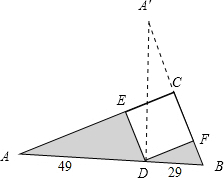 解:如图把△ADE绕点D顺时旋转90°,
解:如图把△ADE绕点D顺时旋转90°,
∵四边形CEDF为正方形,
∴DE=DF,
∴A′、F、B三点在一条直线上,且∠A′DF=∠ADE,
∵∠EDF=90°,
∴∠ADE+∠FDB=90°,
∴∠A′DB=90°,且A′D=AD=49,BD=29,
∴S△A′BD=
A′D•BD=
×49×29=
,
∴S阴影=S△A′DB=
.
 解:如图把△ADE绕点D顺时旋转90°,
解:如图把△ADE绕点D顺时旋转90°,∵四边形CEDF为正方形,
∴DE=DF,
∴A′、F、B三点在一条直线上,且∠A′DF=∠ADE,
∵∠EDF=90°,
∴∠ADE+∠FDB=90°,
∴∠A′DB=90°,且A′D=AD=49,BD=29,
∴S△A′BD=
| 1 |
| 2 |
| 1 |
| 2 |
| 1421 |
| 2 |
∴S阴影=S△A′DB=
| 1421 |
| 2 |
点评:本题主要考查正方形的性质及旋转的应用,利用条件通过旋转把所求阴影部分的面积转化成△A′BD的面积是解题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目

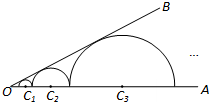 如图,∠AOB=30°,n个半圆依次外切,它们的圆心都在射线OA上并与射线OB相切,设半圆C1、半圆C2、半圆C3…、半圆Cn的半径分别是r1、r2、r3…、rn,则
如图,∠AOB=30°,n个半圆依次外切,它们的圆心都在射线OA上并与射线OB相切,设半圆C1、半圆C2、半圆C3…、半圆Cn的半径分别是r1、r2、r3…、rn,则 如图,已知四边形ABCD为正方形,OB=OC,∠BOC=150°,求证:△AOD为等边三角形.
如图,已知四边形ABCD为正方形,OB=OC,∠BOC=150°,求证:△AOD为等边三角形.