题目内容
 已知:如图,在平面直角坐标系中,Rt△OCD的一边OC在x轴上,∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.
已知:如图,在平面直角坐标系中,Rt△OCD的一边OC在x轴上,∠C=90°,点D在第一象限,OC=3,DC=4,反比例函数的图象经过OD的中点A.(1)求该反比例函数的解析式;
(2)若该反比例函数y=
| k |
| x |
(3)在反比例函数y=
| k |
| x |
考点:反比例函数综合题
专题:
分析:(1)根据已知得出D点坐标为(3,4),得到OD的中点A的坐标为(
,2),利用待定系数法求反比例函数的解析式;
(2)令x=3,则y=
=1,确定B点坐标,然后利用待定系数法求直线AB的解析式;
(3)先求出直线AC的解析式,再分两种情况讨论,当AC∥DE时四边形ACED为梯形,求出DE的解析式,再求出DE与反比例函数的交点即可;当CE∥AD时,四边形ACED为梯形,求出CE的解析式,再求出CE与反比例函数的交点即可.
| 3 |
| 2 |
(2)令x=3,则y=
| 3 |
| 3 |
(3)先求出直线AC的解析式,再分两种情况讨论,当AC∥DE时四边形ACED为梯形,求出DE的解析式,再求出DE与反比例函数的交点即可;当CE∥AD时,四边形ACED为梯形,求出CE的解析式,再求出CE与反比例函数的交点即可.
解答:解:(1)∵OC=3,DC=4,
∴D点坐标为(3,4),
而点A为OD的中点,
∴A点坐标为(
,2),
设反比例函数的解析式为y=
,
把A(
,2)代入得k=2×
=3,
∴反比例函数的解析式为y=
;
(2)令x=3,则y=
=1,
∴点B的坐标为(3,1);
设直线AB的解析式为y=kx+b,
把A(
,2)和B(3,1)代入得,
,
解得k=-
,b=3,
∴直线AB的解析式为y=-
x+3;
(3)设AC的解析式为:y=ax+b,
则
,
解得:
,
则直线AC的解析式为:y=-
x+4,
如图1:当AC∥DE时,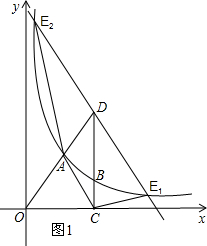
四边形ACED为梯形,
设DE的解析式为:y=-
x+m,
则4=-
×3+m,
解得:m=8,
则DE的解析式为:y=-
x+8,
由
,
解得:
或
;
如图2:当CE∥AD时,四边形ACED为梯形,
∵OD的解析式为y=
x,
∴设CE的解析式为:y=
x+n,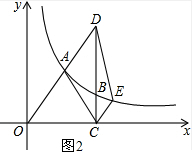
则0=
×3+n,
解得:n=-4,
∴CE的解析式为:y=
x-4,
由
得:
或
(不合题意,舍去);
则E的坐标(
,
)或(
,
)或(
,
-2).
∴D点坐标为(3,4),
而点A为OD的中点,
∴A点坐标为(
| 3 |
| 2 |
设反比例函数的解析式为y=
| k |
| x |
把A(
| 3 |
| 2 |
| 3 |
| 2 |
∴反比例函数的解析式为y=
| 3 |
| x |
(2)令x=3,则y=
| 3 |
| 3 |
∴点B的坐标为(3,1);
设直线AB的解析式为y=kx+b,
把A(
| 3 |
| 2 |
|
解得k=-
| 2 |
| 3 |
∴直线AB的解析式为y=-
| 2 |
| 3 |
(3)设AC的解析式为:y=ax+b,
则
|
解得:
|
则直线AC的解析式为:y=-
| 4 |
| 3 |
如图1:当AC∥DE时,

四边形ACED为梯形,
设DE的解析式为:y=-
| 4 |
| 3 |
则4=-
| 4 |
| 3 |
解得:m=8,
则DE的解析式为:y=-
| 4 |
| 3 |
由
|
解得:
|
|
如图2:当CE∥AD时,四边形ACED为梯形,
∵OD的解析式为y=
| 4 |
| 3 |
∴设CE的解析式为:y=
| 4 |
| 3 |

则0=
| 4 |
| 3 |
解得:n=-4,
∴CE的解析式为:y=
| 4 |
| 3 |
由
|
|
|
则E的坐标(
6+
| ||
| 2 |
12-2
| ||
| 11 |
6-
| ||
| 2 |
12+2
| ||
| 11 |
6+3
| ||
| 4 |
| 7 |
点评:本题考查了反比例函数的综合题的解法:先利用待定系数法确定反比例的解析式,那么图象上所有点的横纵坐标的乘积为定值.也考查了线段中点坐标的求法.

练习册系列答案
相关题目
 如图,把长方形纸片ABCD对折,设折痕为MN,再把B点沿AE折叠,使点B落在折痕MN上,得到点B′,延长EB′交AD于F点,试判断△EAF的形状.
如图,把长方形纸片ABCD对折,设折痕为MN,再把B点沿AE折叠,使点B落在折痕MN上,得到点B′,延长EB′交AD于F点,试判断△EAF的形状. 如图,已知四边形ABCD为正方形,OB=OC,∠BOC=150°,求证:△AOD为等边三角形.
如图,已知四边形ABCD为正方形,OB=OC,∠BOC=150°,求证:△AOD为等边三角形. 如图,AD是△ABC的高,AC=12cm,∠BAD=30°,∠DAC=45°.求AB的长.
如图,AD是△ABC的高,AC=12cm,∠BAD=30°,∠DAC=45°.求AB的长.