题目内容
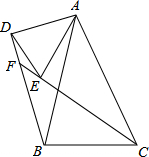 如图,AB=AC,AD=AE,∠DAE=∠BAC=α,CE的延长线交BD于F.
如图,AB=AC,AD=AE,∠DAE=∠BAC=α,CE的延长线交BD于F.(1)求证:BD=CE;
(2)求∠DFC的度数.
考点:全等三角形的判定与性质,等腰三角形的性质
专题:计算题
分析:(1)根据题意得到夹角相等,利用SAS得到三角形DAB与三角形EAC全等,利用全等三角形对应边相等得到BD=CE;
(2)由全等三角形对应角相等得到∠DBA=∠ECA,由AB=AC,利用等边对等角表示出∠ABC与∠ACB,以及∠ABC+∠ACB,利用外角性质及等量代换即可求出∠DFC的度数.
(2)由全等三角形对应角相等得到∠DBA=∠ECA,由AB=AC,利用等边对等角表示出∠ABC与∠ACB,以及∠ABC+∠ACB,利用外角性质及等量代换即可求出∠DFC的度数.
解答:(1)证明:∵∠DAE=∠BAC=α,
∴∠DAB=∠EAC=α+∠EAB,
在△DAB和EAC中,
,
∴△DAB≌△EAC(SAS),
∴BD=CE,∠DBA=∠ECA;
(2)解:∵AB=AC,∠BAC=α,
∴∠ABC=∠ACB=
(180°-α),∠ABC+∠ACB=180°-α,
则∠DFC=∠FBC+∠FCB=∠DBA+∠ABC+∠BCF=∠ABC+∠ECA+∠BCF=∠ABC+∠ACB=180°-α.
∴∠DAB=∠EAC=α+∠EAB,
在△DAB和EAC中,
|
∴△DAB≌△EAC(SAS),
∴BD=CE,∠DBA=∠ECA;
(2)解:∵AB=AC,∠BAC=α,
∴∠ABC=∠ACB=
| 1 |
| 2 |
则∠DFC=∠FBC+∠FCB=∠DBA+∠ABC+∠BCF=∠ABC+∠ECA+∠BCF=∠ABC+∠ACB=180°-α.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案
相关题目

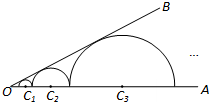 如图,∠AOB=30°,n个半圆依次外切,它们的圆心都在射线OA上并与射线OB相切,设半圆C1、半圆C2、半圆C3…、半圆Cn的半径分别是r1、r2、r3…、rn,则
如图,∠AOB=30°,n个半圆依次外切,它们的圆心都在射线OA上并与射线OB相切,设半圆C1、半圆C2、半圆C3…、半圆Cn的半径分别是r1、r2、r3…、rn,则
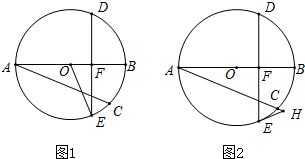 ⊥AB于点F,DE交AC于点G.
⊥AB于点F,DE交AC于点G. 如图,已知四边形ABCD为正方形,OB=OC,∠BOC=150°,求证:△AOD为等边三角形.
如图,已知四边形ABCD为正方形,OB=OC,∠BOC=150°,求证:△AOD为等边三角形. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示.
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示.