题目内容
12. 如图,若OD、OE分别为∠BOA与∠COA的角平分线且∠BOE=14°,∠COD=88°,求∠AOC的度数.
如图,若OD、OE分别为∠BOA与∠COA的角平分线且∠BOE=14°,∠COD=88°,求∠AOC的度数.
分析 设∠DOA=x,则∠BOD=x,从而得到∠AOC=88°+x,故此∠AOE=$\frac{1}{2}(88°+x)$,由∠EOB=∠EOA-∠BOA可得到关于x的方程,从而可求得x的值,然后可求得∠AOC的度数.
解答 解:∵OD是∠BOA的平分线,
∴∠BOD=∠AOD.
设∠DOA=x,则∠BOD=x,∠AOC=88°+x.
∵OE是∠COA的平分线,
∴∠EOA=$\frac{1}{2}∠COA$=$\frac{1}{2}(88°+x)$.
∵∠EOB=∠EOA-∠BOA,
∴$\frac{1}{2}(88°+x)$-2x=14°.
解得:x=20°.
∴∠AOC=88°+20°=108°.
点评 本题主要考查的是角平分线、角的比较与运算,根据图中角的和差关系列出关于x的方程是解题的关键.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
20.如果x,y都不为零,且2x=3y,那么下列比例中正确的是( )
| A. | $\frac{x}{y}=\frac{2}{3}$ | B. | $\frac{x}{3}=\frac{y}{2}$ | C. | $\frac{x}{2}=\frac{3}{y}$ | D. | $\frac{x}{3}=\frac{2}{y}$ |
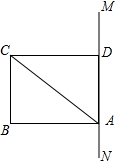 如图,已知矩形ABCD的边AD在直线MN上,BC=6,AB=8,点E是直线MN上的一个动点,若以AB为半径的⊙A与以ED为半径的⊙E相切,求⊙E的半径.
如图,已知矩形ABCD的边AD在直线MN上,BC=6,AB=8,点E是直线MN上的一个动点,若以AB为半径的⊙A与以ED为半径的⊙E相切,求⊙E的半径.