Question

3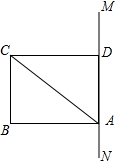．如图，已知矩形ABCD的边AD在直线MN上，BC=6，AB=8，点E是直线MN上的一个动点，若以AB为半径的⊙A与以ED为半径的⊙E相切，求⊙E的半径．

Answer 1

分析 根据相切两圆的性质得出两圆相切时切点是直线MN和⊙A的交点，画出两种情况，求出DE的长即可．

解答 解：∵四边形ABCD是矩形，AB=8，BC=6，
∴BC=AD=6，⊙A的半径为8，
∴点D在⊙A的内部，
∵点E是直线MN上的一个动点，若以AB为半径的⊙A与以ED为半径的⊙E相切，
∴两圆相切时切点是直线MN和⊙A的交点，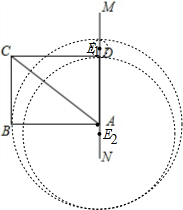

如图，有两种情况：当圆心是E₁时，DE=$\frac{1}{2}$×（8-6）=1；
当圆心是E₂时，DE=$\frac{1}{2}$×（6+8）=7，
即⊙E的半径是1或7．

点评 本题考查了矩形的性质，相切两圆的性质的应用，能求出符合条件的所有情况是解此题的关键．