题目内容
15.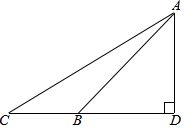 如图,长4m的楼梯AB的倾斜角∠ABD为45°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为30°,求调整后的楼梯AC的长.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
如图,长4m的楼梯AB的倾斜角∠ABD为45°,为了改善楼梯的安全性能,准备重新建造楼梯,使其倾斜角∠ACD为30°,求调整后的楼梯AC的长.(精确到0.1m,$\sqrt{2}$≈1.41,$\sqrt{3}$≈1.73)
分析 先在Rt△ABD中利用正弦的定义计算出AD,然后在Rt△ACD中利用正弦的定义计算AC即可.
解答 解:在Rt△ADB中,∵sin∠ABD=$\frac{AD}{AB}$,
∴AD=4sin45°=$2\sqrt{2}$(m),
在Rt△ACD中,∵sin∠ACD=$\frac{AD}{AC}$,
∴AC=$4\sqrt{2}=4×1.41=5.64≈5.6$(m).
答:调整后的楼梯AC的长约为5.6 m.
点评 本题考查了解直角三角形的实际应用中的坡度坡角问题,难度不大,注意细心运算即可.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案
相关题目
5.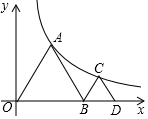 如图:△ADB、△BCD均为等边三角形,若点顶点A、C均在反比例函数y=$\frac{k}{x}$上,若C的坐标点(a、$\sqrt{3}$),则k的值为( )
如图:△ADB、△BCD均为等边三角形,若点顶点A、C均在反比例函数y=$\frac{k}{x}$上,若C的坐标点(a、$\sqrt{3}$),则k的值为( )
 如图:△ADB、△BCD均为等边三角形,若点顶点A、C均在反比例函数y=$\frac{k}{x}$上,若C的坐标点(a、$\sqrt{3}$),则k的值为( )
如图:△ADB、△BCD均为等边三角形,若点顶点A、C均在反比例函数y=$\frac{k}{x}$上,若C的坐标点(a、$\sqrt{3}$),则k的值为( )| A. | 2$\sqrt{3}$ | B. | 3$\sqrt{3}$+$\sqrt{6}$ | C. | 3$\sqrt{3}$+2$\sqrt{6}$ | D. | 2$\sqrt{6}$ |
6.-$\sqrt{3}$的相反数为( )
| A. | $\sqrt{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | 3 | D. | -3 |
10.下列运算正确的是( )
| A. | a2+a2=a4 | B. | (a+b)2=a2+b2 | C. | $\sqrt{9}$=±3 | D. | (-a2)3=-a6 |
20.下列运算正确的是( )
| A. | a3•a4=a7 | B. | (3a-b)2=9a2-b2 | C. | (ab)3=ab3 | D. | 4a-3a=1 |
14.已知2:x=3:9,则x=( )
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
 如图,在△ABC中,AB=AC,∠ABC的平分线与△ABC的外角平分线相交于点D,若∠BDC=25°,则∠ABC的度数为65°.
如图,在△ABC中,AB=AC,∠ABC的平分线与△ABC的外角平分线相交于点D,若∠BDC=25°,则∠ABC的度数为65°.