题目内容
16.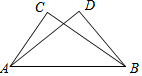 如图,已知∠ACB=∠ADB=90°,AC=BD.又因为公共边AB=BA,所以△ABC≌△BAD,其理由是( )
如图,已知∠ACB=∠ADB=90°,AC=BD.又因为公共边AB=BA,所以△ABC≌△BAD,其理由是( )| A. | SAS | B. | ASA | C. | SSA | D. | HL |
分析 HL指的是:斜边与直角边对应相等的两个直角三角形全等,由此可得出答案.
解答 解:AB=AB(公共边),△ABC和△ABD都是直角三角形,且AC=BD,
可以用“HL”来说明△ABC≌△BAD,
故选D.
点评 本题考查了全等三角形的判定,解答本题需要同学们理解HL判定定理的内容.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
6. 如图,直线AB、CD相交于点O,OE⊥OF,OD平分∠AOE,下列结论:
如图,直线AB、CD相交于点O,OE⊥OF,OD平分∠AOE,下列结论:
①∠BOE的余角是∠AOE,补角是∠BOF
②∠AOD=∠DOE=$\frac{1}{2}$∠AOE
③∠BOE=2∠COF
④∠BOF=∠COF
其中正确的有( )
 如图,直线AB、CD相交于点O,OE⊥OF,OD平分∠AOE,下列结论:
如图,直线AB、CD相交于点O,OE⊥OF,OD平分∠AOE,下列结论:①∠BOE的余角是∠AOE,补角是∠BOF
②∠AOD=∠DOE=$\frac{1}{2}$∠AOE
③∠BOE=2∠COF
④∠BOF=∠COF
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
1.下列关于变量x,y的关系,其中y不是x的函数的是( )
| A. | 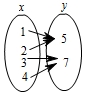 | B. | 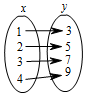 | C. | 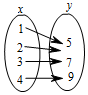 | D. | 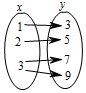 |
8.已知一条圆弧的度数为60°,弧长为10π,则此圆弧的半径为( )
| A. | 15 | B. | 30 | C. | $\sqrt{30}$ | D. | 15π |
6.己知二次函数y=ax2+bx+c(a>0),对任意实数t,其图象都经过点(2+t,m)和点(2-t,m),又图象经过点(-1,y1),(2,y2),(6,y3),则函数值y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y3>y1>y2 | C. | y2>y1>y3 | D. | y3>y2>y1 |
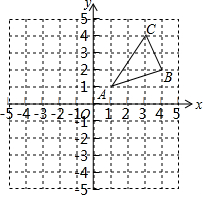 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).