题目内容
17.证明命题“等腰三角形底边上的中点到两腰的距离相等”是真命题.分析 作出图形,连接AD,由AB=AC,D为BC中点,利用等腰三角形的“三线合一”性质得到AD为顶角的平分线,由DE与AB垂直,DF与AC垂直,根据角平分线上的点到角两边的距离相等即可得到DE=DF,得证.
解答 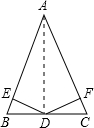 已知:如图,AB=AC,D是BC中点,DE⊥AB,DF⊥AC,
已知:如图,AB=AC,D是BC中点,DE⊥AB,DF⊥AC,
求证:DE=DF,
证明:连接AD,
∵AB=AC,D是BC中点,
∴AD为∠BAC的角平分线(三线合一的性质),
又∵DE⊥AB,DF⊥AC,
∴DE=DF(角平分线上的点到角的两边相等).
点评 本题主要考查命题的真假判断,正确的命题叫真命题,错误的命题叫做假命题.判断命题的真假关键是要熟悉课本中的性质定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
8.已知一条圆弧的度数为60°,弧长为10π,则此圆弧的半径为( )
| A. | 15 | B. | 30 | C. | $\sqrt{30}$ | D. | 15π |
12.若直线y=kx+b是由直线y=2x+4沿x轴向右平移4个单位所得,则k,b的值分别是( )
| A. | k=-2,b=-4 | B. | k=2,b=-4 | C. | k=-4,b=2 | D. | k=4,b=2 |
2.下列事件中属于必然事件的是( )
| A. | 任意买一张电影票,座位号是偶数 | B. | 367人中至少有2人的生日相同 | ||
| C. | 掷一次骰子,向上的一面是6点 | D. | 某射击运动员射击1次,命中靶心 |
6.己知二次函数y=ax2+bx+c(a>0),对任意实数t,其图象都经过点(2+t,m)和点(2-t,m),又图象经过点(-1,y1),(2,y2),(6,y3),则函数值y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y3>y1>y2 | C. | y2>y1>y3 | D. | y3>y2>y1 |
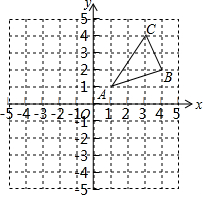 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).