题目内容
11. 如图,在△ABC,AC的长为8cm,AC边上的高为BD,当B点在线段BD上向D点运动时,△ABC的面积发生了变化.
如图,在△ABC,AC的长为8cm,AC边上的高为BD,当B点在线段BD上向D点运动时,△ABC的面积发生了变化.(1)指出在此变化过程中的变量;
(2)当高BD从6cm变化到2cm时,△ABC的面积S的变化范围;
(3)若BD=6cm,BD上有一动点P沿射线BD匀速运动,速度为1cm/s,指出△PAC的面积y(cm2)与P点运动时间t之间的关系,并求出当S△PAC=$\frac{1}{3}$S△ABC时的t值.
分析 (1)由题意根据常量和变量的定义,可得到再点B沿BD所在直线向点D运动时,三角形的面积和高BD发生了变化,即可得到变量;
(2)由题意可知,△ABC的面积=$\frac{1}{2}$AC×BD,把BD=6cm和BD=2cm分别代入面积公式,即可得到三角形的面积的变化范围;
(3)利用三角形的面积公式即可得到关系式.
解答  解:(1)由题意和图形知,
解:(1)由题意和图形知,
∵点B沿BD所在直线向点D运动,
∴BD的长度在逐渐变短,
∴线段BD是变化的量,
∵高BD变化,所以面积也在变化,
故变量为线段BD,因变量是△ABC的面积;
(2)由题意可知,△ABC的面积=$\frac{1}{2}$AC×BD,
把BD=6cm代入,得△ABC的面积=$\frac{1}{2}$×8×6=24cm2,
把BD=2cm代入,得△ABC的面积=$\frac{1}{2}$×8×2=8cm2,
∴三角形的面积S的变化范围为:8cm2≤S≤24cm2;
(3)∵BD上有一动点P沿射线BD匀速运动,速度为1cm/s,
∴PD=t,
∴△PAC的面积y=$\frac{1}{2}$×8t=4t,
∴y与x的关系式为:y=4x、t,
当S△PAC=$\frac{1}{3}$S△ABC时,4t=$\frac{1}{3}$×$\frac{1}{2}$×6×8,
解得t=2.
点评 本题主要考查了函数关系式,常量与变量,函数值及三角形的面积,解题的关键是能求出y与x的关系式.

练习册系列答案
相关题目
1.下列关于变量x,y的关系,其中y不是x的函数的是( )
| A. | 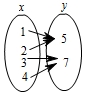 | B. | 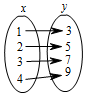 | C. | 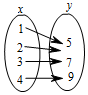 | D. | 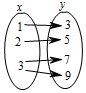 |
2.下列事件中属于必然事件的是( )
| A. | 任意买一张电影票,座位号是偶数 | B. | 367人中至少有2人的生日相同 | ||
| C. | 掷一次骰子,向上的一面是6点 | D. | 某射击运动员射击1次,命中靶心 |
6.己知二次函数y=ax2+bx+c(a>0),对任意实数t,其图象都经过点(2+t,m)和点(2-t,m),又图象经过点(-1,y1),(2,y2),(6,y3),则函数值y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y3>y1>y2 | C. | y2>y1>y3 | D. | y3>y2>y1 |
16.符号[x]表示不超过x的最大整数,例如[2.6]=2,[-1]=-1,[-2.6]=-3.若关于x的方程[x]+[3x]=kx(k≠0)在0<x<1内有解,则k的取值范围是( )
| A. | $\frac{3}{2}$<k≤3 | B. | 2<k≤3 | C. | 2≤k≤3 | D. | $\frac{3}{2}$<k≤2 |
3.将5041精确到百位的结果是( )
| A. | 5000 | B. | 5.0×103 | C. | 50 | D. | 5.04×103 |
1.计算sin45°的值等于( )
| A. | $\sqrt{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | $\frac{\sqrt{3}}{2}$ |
 如图,在正方形ABCD的对角线BD上取点E,使得∠BAE=75°,连接AE,CE,将线段CE绕点C顺时针旋转,使点E的对应点恰好落在AE延长线上的点F处.若AB=2,则AF的长为$\frac{4\sqrt{6}}{3}$.
如图,在正方形ABCD的对角线BD上取点E,使得∠BAE=75°,连接AE,CE,将线段CE绕点C顺时针旋转,使点E的对应点恰好落在AE延长线上的点F处.若AB=2,则AF的长为$\frac{4\sqrt{6}}{3}$.