题目内容
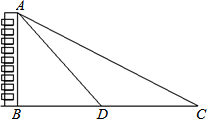
5. 已知:如图,∠B=∠1,AE⊥AD,∠D=75°,求∠2的度数.
已知:如图,∠B=∠1,AE⊥AD,∠D=75°,求∠2的度数.
分析 证出AB∥CD,由平行线的性质得出∠BAD+∠D=180°,求出∠BAD=105°,由垂线的性质得出∠DAE=90°,即可求出∠2的度数.
解答 解:∵∠B=∠1,
∴AB∥CD,
∴∠BAD+∠D=180°,
∵∠D=75°
∴∠BAD=180°-75°=105°,
∵AE⊥AD,
∴∠DAE=90°,
∵∠2+∠DAE=∠BAD,
∴∠2=105°-90°=15°.
点评 本题考查了平行线的判定与性质、垂线的定义;熟练掌握平行线的判定与性质是解决问题的关键.

练习册系列答案
 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
15.下列计算中,不正确的是( )
| A. | a2•a5=a10 | B. | a2-2ab+b2=(a-b)2 | C. | -(a-b)=b-a | D. | 3a3b2÷a2b2=3a |
16.下列二次根式中,最简二次根式是( )
| A. | $\sqrt{x-1}$ | B. | $\sqrt{18}$ | C. | $\sqrt{\frac{1}{16}}$ | D. | $\sqrt{9{a^2}}$ |
13.下列各组中,不是同类项的是( )
| A. | 2πR与π2R | B. | -x2y与2yx2 | C. | $\frac{1}{2}$ab2与a2b | D. | 35与53 |
10.用因式分解法把方程5m(m-3)=3-m分解成两个一次方程,正确的是( )
| A. | m-3=0,5m-1=0 | B. | 3-m=0,5m=0 | C. | 5m+1=0,m-3=0 | D. | 5m=0,m-3=0 |
15.在平面直角坐标系中,若点A(a,b)在第一象限内,则点B(a,-b)所在的象限( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 如图,为了测量某建筑物AB高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进12m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB高度等于(6$\sqrt{3}$+6)m.
如图,为了测量某建筑物AB高度,在平地上C处测得建筑物顶端A的仰角为30°,沿CB方向前进12m到达D处,在D处测得建筑物顶端A的仰角为45°,则建筑物AB高度等于(6$\sqrt{3}$+6)m.