题目内容
13.上午某时,将一根1米长的木棒按铅垂方向竖立在平地上,木棒在平地上的投影长为0.75米,同一时刻,将一根1.2米长的木棒按铅垂方向竖立在坡度为1:5的斜坡上,且木棒的投影完全落在坡面上,则该投影长为$\frac{18\sqrt{26}}{115}$米.分析 作BE⊥CD于E,根据坡度的概念用BE表示出DE,根据题意用BE表示出CE,根据1.2米长的木棒列出方程,求出BE,根据勾股定理计算即可.
解答 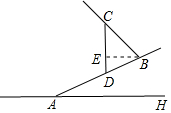 解:作BE⊥CD于E,
解:作BE⊥CD于E,
则BE∥AH,
∴DE=$\frac{1}{5}$BE,
由题意得,$\frac{CE}{BE}$=$\frac{1}{0.75}$=$\frac{4}{3}$,
∴CE=$\frac{4}{3}$BE,
则$\frac{1}{5}$BE+$\frac{4}{3}$BE=1.2,
解得,BE=$\frac{18}{23}$,
由勾股定理得,BD=$\sqrt{B{E}^{2}+D{E}^{2}}$=$\frac{18\sqrt{26}}{115}$米,
故答案为:$\frac{18\sqrt{26}}{115}$米.
点评 本题考查的是解直角三角形的应用-坡度坡角问题,掌握坡度的概念、熟记锐角三角函数的定义是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目