题目内容
18.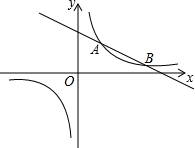 如图,一次函数,一次函数y=kx+5(k为常数,k≠0)的图象与反比例函数$y=\frac{8}{x}$的图象相交于A(2,b),B两点.
如图,一次函数,一次函数y=kx+5(k为常数,k≠0)的图象与反比例函数$y=\frac{8}{x}$的图象相交于A(2,b),B两点.(1)求一次函数的表达式;
(2)若将直线AB向下平移m(m>0)个单位长度后与反比例函数的图象只有一个公共交点,求m的值.
分析 (1)先利用反比例函数解析式代入$y=\frac{8}{x}$求出b=4,得到A点坐标为(2,4),然后把A点坐标代入y=kx+5中求出k,从而得到一次函数解析式为y=-$\frac{1}{2}$x+5;
(2)由于将直线AB向下平移m(m>0)个单位长度得直线解析式为y=-$\frac{1}{2}$x+5-m,则直线y=-$\frac{1}{2}$x+5-m与反比例函数有且只有一个公共点,即方程$\frac{8}{x}$=-$\frac{1}{2}$x+5-m只有一组解,再根据判别式的意义得到关于m的方程,最后解方程求出m的值.
解答 解:(1)把A(2,b)代入$y=\frac{8}{x}$得b=$\frac{8}{2}$=4,
所以A点坐标为(2,4),
把A(2,4)代入y=kx+5得2k+5=4,解得k=-$\frac{1}{2}$,
所以一次函数解析式为y=-$\frac{1}{2}$x+5;
(2)将直线AB向下平移m(m>0)个单位长度得直线解析式为y=-$\frac{1}{2}$x+5-m,
∵直线AB向下平移m(m>0)个单位长度后与反比例函数的图象只有一个公共交点,
∴$\frac{8}{x}$=-$\frac{1}{2}$x+5-m,
整理得x2-2(m-5)x+16=0,
△=[2(m-5)]2-4×1×16=0,解得m=9或m=1,
即m的值为1或9.
点评 本题考查了反比例函数与一次函数的交点问题:求反比例函数与一次函数的交点坐标,把两个函数关系式联立成方程组求解,若方程组有解则两者有交点,方程组无解,则两者无交点.也考查了一次函数与几何变换.

练习册系列答案
相关题目
6.下面表格列出了函数y=ax2+bx+c(a,b、c是常数,且a≠0),部分x与y对应值,那么方程ax2+bx+c=0的一个根x的取值范围是( )
| x | 6.17 | 6.18 | 6.19 | 6.20 |
| y | -0.03 | -0.01 | 0.02 | 0.04 |
| A. | 6<x<6.7 | B. | 6.7<x<6.18 | C. | 6.18<x<6.19 | D. | 6.9<x<9.20 |
13.使分式$\frac{1-x}{x}$有意义的x的取值范围是( )
| A. | x>1 | B. | x<1 | C. | x≠0 | D. | x<1且x≠0 |
3.计算-$\frac{1}{3}$a2•(-6ab)的结果正确的是( )
| A. | -2a3b | B. | 2a3b | C. | -2a2b | D. | 2a2b |
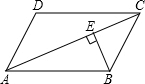 如图所示,在?ABCD中,AC=21cm,BE⊥AC于E,且BE=5cm,AD=7cm,则两条平行线AD与BC间的距离为15cm.
如图所示,在?ABCD中,AC=21cm,BE⊥AC于E,且BE=5cm,AD=7cm,则两条平行线AD与BC间的距离为15cm.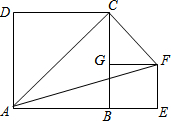 如图,正方形ABCD的边长为a,正方形BEFG的边长为b,
如图,正方形ABCD的边长为a,正方形BEFG的边长为b,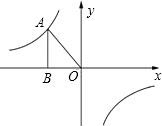 如图所示,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,m),过点A作AB⊥x轴于点B,且△AOB的面积为2$\sqrt{3}$.
如图所示,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,m),过点A作AB⊥x轴于点B,且△AOB的面积为2$\sqrt{3}$.