题目内容
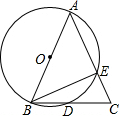 如图,在△ABC中,AB=AC,∠BAC=45°,以AB为直径的⊙O交BC于点D,交AC于点E.
如图,在△ABC中,AB=AC,∠BAC=45°,以AB为直径的⊙O交BC于点D,交AC于点E.(1)求∠EBC的度数;
(2)求证:BD=CD.
考点:圆周角定理,全等三角形的判定与性质,等腰三角形的性质
专题:计算题
分析:(1)根据等腰三角形的性质得∠ABC=∠C,再利用三角形内角和计算出∠C=
(180°-∠BAC)=67.5°,接着根据圆周角定理得∠AEB=90°,然后利用三角形外角性质求∠EBC的度数;
(2)连结AD,如图,根据圆周角定理得∠ADB=90°,则AD⊥BC,然后根据等腰三角形的性质即可得到BD=CD.
| 1 |
| 2 |
(2)连结AD,如图,根据圆周角定理得∠ADB=90°,则AD⊥BC,然后根据等腰三角形的性质即可得到BD=CD.
解答: (1)解:∵AB=AC,
(1)解:∵AB=AC,
∴∠ABC=∠C,
∴∠C=
(180°-∠BAC)=
(180°-45°)=67.5°,
∵AB为直径,
∴∠AEB=90°,
∵∠AEB=∠EBC+∠C,
∴∠EBC=90°-67.5°=22.5°;
(2)证明:连结AD,如图,
∵AB为直径,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD.
 (1)解:∵AB=AC,
(1)解:∵AB=AC,∴∠ABC=∠C,
∴∠C=
| 1 |
| 2 |
| 1 |
| 2 |
∵AB为直径,
∴∠AEB=90°,
∵∠AEB=∠EBC+∠C,
∴∠EBC=90°-67.5°=22.5°;
(2)证明:连结AD,如图,
∵AB为直径,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴BD=CD.
点评:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.推论:半圆(或直径)所对的圆周角是直角,90°的圆周角所对的弦是直径.也考查了等腰三角形的性质.

练习册系列答案
相关题目
 如图,在⊙O中,直径AB⊥弦CD,垂足为点E,若AC=2
如图,在⊙O中,直径AB⊥弦CD,垂足为点E,若AC=2| 3 |
| A、30° | B、45° |
| C、60° | D、90° |
 如图,△ABC中,∠C=90°,DE是AB的垂直平分线,∠CAD=2∠DAB,求∠B的度数.
如图,△ABC中,∠C=90°,DE是AB的垂直平分线,∠CAD=2∠DAB,求∠B的度数. 如图,在△ABC中,∠A=70°,直线DE分别与AB,AC相交于D,E,求∠1+∠2的值.
如图,在△ABC中,∠A=70°,直线DE分别与AB,AC相交于D,E,求∠1+∠2的值.