题目内容
如图，△ABC中，∠C=90°，DE是AB的垂直平分线，∠CAD=2∠DAB，求∠B的度数．考点：线段垂直平分线的性质
专题：
分析：由DE是AB的垂直平分线，利用线段的垂直平分线的性质得∠B=∠BAD，结合∠CAD=2∠DAB与直角三角形两锐角互余，可以得到答案．
解答：解：在Rt△ABC中
∵DE是AB的垂直平分线
∴AD=BD
∴∠B=∠BAD
∵∠CAD=2∠DAB，且∠B+∠BAD+∠CAD=90°，
∴4∠B=90°
∴∠B=22.5°．
∵DE是AB的垂直平分线
∴AD=BD
∴∠B=∠BAD
∵∠CAD=2∠DAB，且∠B+∠BAD+∠CAD=90°，
∴4∠B=90°
∴∠B=22.5°．
点评：此题主要考查线段的垂直平分线的性质等几何知识．线段的垂直平分线上的点到线段的两个端点的距离相等．由已知条件得出4∠B=90°是正确解答本题的关键．
练习册系列答案
相关题目
如图是用棋子摆成的“上”字：
如果按照以上规律继续摆下去，那么通过观察，第n个“上”字需用棋子的枚数是（ ）
如果按照以上规律继续摆下去，那么通过观察，第n个“上”字需用棋子的枚数是（ ）
| A、n+5 | B、2n+3 |
| C、4n+2 | D、5n+1 |
如图，从A地到B地的公路需经过C地，图中AC=10千米，∠CAB=25°，∠CBA=37°，因城市规划的需要，将在A、B两地之间修建一条笔直的公路．
如图的扇形统计图反映了小明家一年的开支情况，则此扇形统计图中“体育”部分所在的扇形的圆心角度数为
如图，已知点D、E是△ABC的边BC上两点，且BD=CE，∠1=∠2．试证：△ABD≌△ACE．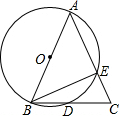
如图，在△ABC中，AB=AC，∠BAC=45°，以AB为直径的⊙O交BC于点D，交AC于点E．