题目内容

如图，在⊙O中，直径AB⊥弦CD，垂足为点E，若AC=2
3
，AE=3，则劣弧BD的度数是（　　）
A、30°B、45°
C、60°D、90°
考点：圆周角定理,垂径定理,特殊角的三角函数值
专题：
分析：先根据垂径定理得出
BC
=
BD
，再由直径AB⊥弦CD，AC=2
3
，AE=3求出∠CAE的度数，进而可得出结论．
解答：解：∵直径AB⊥弦CD，
∴
BC
=
BD
．
∵AC=2
3
，AE=3，
∴cos∠CAE=
AE
AC
=
3
2
3
=
3
2
，
∴∠CAE=30°，
∴
BC
=
BD
=30°．
故选A．
点评：本题考查的是圆周角定理，熟知在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半是解答此题的关键．
练习册系列答案
相关题目
解方程：
（1）
1+
9
4x
-2
x
4x+9
=
3
2
．
（2）2x2-4x+3
x2-2x+6
=15．
点P（-4，-3）到坐标原点O的距离是
 
．
如图的扇形统计图反映了小明家一年的开支情况，则此扇形统计图中“体育”部分所在的扇形的圆心角度数为
 
度．
已知a-b=-2，则代数式a-b-3的值是（　　）
A、-1B、1C、-5D、5
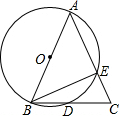如图，在△ABC中，AB=AC，∠BAC=45°，以AB为直径的⊙O交BC于点D，交AC于点E．
（1）求∠EBC的度数；
（2）求证：BD=CD．
解方程：2-
2x+1
3
=
1+x
2
．
分式方程
2
x-1
=
3
x+1
的解为（　　）
A、2B、3C、5D、无解
如图，在△ABC中，∠ABC与∠ACB的平分线相交于O点．若∠ABC+∠ACB=130°，求∠BOC的度数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网