题目内容
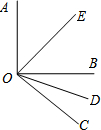 已知,如图,∠AOB=90°,∠EOD=70°,OE、OD分别是∠AOB和∠BOC的角平分线,求∠BOC的度数.
已知,如图,∠AOB=90°,∠EOD=70°,OE、OD分别是∠AOB和∠BOC的角平分线,求∠BOC的度数.考点:角平分线的定义
专题:
分析:先由∠AOB=90°,OE是∠AOB的角平分线,得出∠EOB=
∠AOB=45°,那么∠BOD=∠EOD-∠EOB=70°-45°=25°,再由OD是∠BOC的角平分线,得出∠BOC=∠BOD=50°.
| 1 |
| 2 |
解答:解:∵∠AOB=90°,OE是∠AOB的角平分线,
∴∠EOB=
∠AOB=45°,
∵∠EOD=70°,
∴∠BOD=∠EOD-∠EOB=70°-45°=25°,
∵OD是∠BOC的角平分线,
∴∠BOC=∠BOD=50°.
∴∠EOB=
| 1 |
| 2 |
∵∠EOD=70°,
∴∠BOD=∠EOD-∠EOB=70°-45°=25°,
∵OD是∠BOC的角平分线,
∴∠BOC=∠BOD=50°.
点评:本题考查了角的计算及角平分线的定义,首先确定各角之间的关系,利用角平分线的性质来求.

练习册系列答案
相关题目
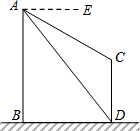 如图,AB、CD为两个建筑物,建筑物AB的高度为80m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为69°.
如图,AB、CD为两个建筑物,建筑物AB的高度为80m,从建筑物AB的顶部A点测得建筑物CD的顶部C点的俯角∠EAC为30°,测得建筑物CD的底部D点的俯角∠EAD为69°. 如图,图①所示的正方体木块,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,分别画出②从正面看、从左面看和从上面看到的平面图形.
如图,图①所示的正方体木块,沿其相邻三个面的对角线(图中虚线)剪掉一角,得到如图②的几何体,分别画出②从正面看、从左面看和从上面看到的平面图形.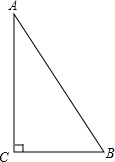 已知,在△ABC中,∠C=90°,sinA=
已知,在△ABC中,∠C=90°,sinA=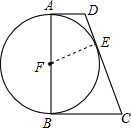 如图:在直角梯形四ABCD中,AD∥BC,∠B=90°,以AB为直径的⊙F切DC于点E.若⊙F的半径是6cm,AD=4cm,求梯形ABCD的面积.
如图:在直角梯形四ABCD中,AD∥BC,∠B=90°,以AB为直径的⊙F切DC于点E.若⊙F的半径是6cm,AD=4cm,求梯形ABCD的面积.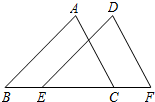 己知:如图,点E、C在线段BF上,BE=CF,AB∥DE,AC∥DF.求证:△ABC≌△DEF.
己知:如图,点E、C在线段BF上,BE=CF,AB∥DE,AC∥DF.求证:△ABC≌△DEF.
 如图,AB与CD交于点E,CF为∠BCD的平分线,AF为∠BAD的平分线.
如图,AB与CD交于点E,CF为∠BCD的平分线,AF为∠BAD的平分线.