题目内容
 如图,AB与CD交于点E,CF为∠BCD的平分线,AF为∠BAD的平分线.
如图,AB与CD交于点E,CF为∠BCD的平分线,AF为∠BAD的平分线.(1)∠F与∠B、∠D之间的关系;
(2)若∠B:∠D:∠F=2:4:x,求x的值.
考点:三角形内角和定理,三角形的外角性质
专题:
分析:(1)根据角平分线定义得出∠1=∠2,∠3=∠4,根据三角形内角和定理得出∠D+∠1=∠F+∠3,∠B+∠4=∠F=+∠2,两边相加整理即可得出答案;
(2)根据已知和∠B+∠D=2∠F得出方程,求出方程的解即可.
(2)根据已知和∠B+∠D=2∠F得出方程,求出方程的解即可.
解答:解:(1)如图,

∠B+∠D=2∠F,
理由是:∵CF为∠BCD的平分线,AF为∠BAD的平分线,
∴∠1=∠2,∠3=∠4,
∴∠D+∠1=∠F+∠3,∠B+∠4=∠F=+∠2,
∴∠B+∠D+∠1+∠4=2∠F+∠2+∠3,
∴∠B+∠D=2∠F;
(2)∵∠B:∠D:∠F=2:4:x,∠B+∠D=2∠F,
∴2+4=2x,
∴x=3.

∠B+∠D=2∠F,
理由是:∵CF为∠BCD的平分线,AF为∠BAD的平分线,
∴∠1=∠2,∠3=∠4,
∴∠D+∠1=∠F+∠3,∠B+∠4=∠F=+∠2,
∴∠B+∠D+∠1+∠4=2∠F+∠2+∠3,
∴∠B+∠D=2∠F;
(2)∵∠B:∠D:∠F=2:4:x,∠B+∠D=2∠F,
∴2+4=2x,
∴x=3.
点评:本题考查的是三角形内角和定理以及角平分线的性质,熟知三角形的内角和等于180°是解答此题的关键.

练习册系列答案
 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目
 如图,在数轴上有a,b两个实数,则下列结论中,正确的是( )
如图,在数轴上有a,b两个实数,则下列结论中,正确的是( )| A、a>-b |
| B、|a|<|b| |
| C、-ab>0 |
| D、a+b>0 |
已知
=
=
=k,则k的取值为( )
| a |
| b+c |
| b |
| c+a |
| c |
| b+a |
A、
| ||
| B、-1 | ||
C、
| ||
D、-
|
 如图是一个物体的俯视图,则它所对应的物体是( )
如图是一个物体的俯视图,则它所对应的物体是( )A、 |
B、 |
C、 |
D、 |
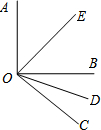 已知,如图,∠AOB=90°,∠EOD=70°,OE、OD分别是∠AOB和∠BOC的角平分线,求∠BOC的度数.
已知,如图,∠AOB=90°,∠EOD=70°,OE、OD分别是∠AOB和∠BOC的角平分线,求∠BOC的度数. 如图,Rt△ABC≌△CDE,∠B=∠D=90°,且B、C、D三点在同一条直线上,试利用这个图形证明勾股定理公式.
如图,Rt△ABC≌△CDE,∠B=∠D=90°,且B、C、D三点在同一条直线上,试利用这个图形证明勾股定理公式. 已知实数a在数轴上的位置如图1所示,则化简
已知实数a在数轴上的位置如图1所示,则化简