题目内容
2.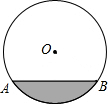 排水管的截面为如图所示的⊙O,半径为5m,如果圆心O到水面的距离是3m,那么水面宽AB=8m.
排水管的截面为如图所示的⊙O,半径为5m,如果圆心O到水面的距离是3m,那么水面宽AB=8m.
分析 过O点作OC⊥AB,连接OB,由垂径定理可得出AB=2BC,在Rt△OBC中利用勾股定理即可得出BC的长,进而可得出AB的长.
解答 解:过O点作OC⊥AB,连接OB,如图所示:
∴AB=2BC,
在Rt△OBC中,BC2+OC2=OB2,
∵OB=5m,OC=3m,
∴BC=$\sqrt{O{B}^{2}-O{C}^{2}}$=4m,
∴AB=2BC=8m.
即水面宽AB为8m;
故答案为:8.
点评 本题考查的是垂径定理及勾股定理,根据题意作出辅助线,构造出直角三角形是解答此题的关键.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
13.下面计算正确的是( )
| A. | 6a-5a=1 | B. | 2(a+b)=2a+b | C. | a+2a2=3a3 | D. | -(a-b)=-a+b |
14.抛物线y=x2-6x+2的顶点坐标是( )
| A. | (3,2) | B. | (-3,7) | C. | (3,-7) | D. | (6,2) |
11.2015年“十一”黄金周,全市累计接待游客近4500000人次,用科学记数法表示4500000这个数是( )
| A. | 4.5×106 | B. | 0.45×107 | C. | 45×105 | D. | 4.5×105 |
 如图,AB是⊙O的直径,点C是⊙O上一点,过点C作⊙O的切线PC交AB的延长线于点P,过点A作AD⊥PC于点D,连接AC,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,过点C作⊙O的切线PC交AB的延长线于点P,过点A作AD⊥PC于点D,连接AC,弦CE平分∠ACB,交AB于点F,连接BE. 如图,在正方形ABCD中,AE⊥DE,AE=12,DE=5,则阴影部分的面积为139.
如图,在正方形ABCD中,AE⊥DE,AE=12,DE=5,则阴影部分的面积为139.
 如图,O是直线AB上一点,已知∠AOC=50°,OD平分∠AOC.
如图,O是直线AB上一点,已知∠AOC=50°,OD平分∠AOC.