题目内容
10. 如图,在正方形ABCD中,AE⊥DE,AE=12,DE=5,则阴影部分的面积为139.
如图,在正方形ABCD中,AE⊥DE,AE=12,DE=5,则阴影部分的面积为139.
分析 由勾股定理求出AD2,阴影部分的面积=正方形ABCD的面积-△ADE的面积,即可得出结果.
解答 解:∵AE⊥DE,AE=12,DE=5,
∴AD2=AE2+DE2=122+52=169,
∵四边形ABCD是正方形,
∴阴影部分的面积=正方形ABCD的面积-△ADE的面积
=AD2-$\frac{1}{2}$AE×DE
=169-$\frac{1}{2}$×12×5
=169-30
=139;
故答案为:139.
点评 本题考查了正方形的性质、勾股定理、三角形面积的计算;熟练掌握正方形的性质,由勾股定理求出AD2是解决问题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
1. 如图,AB是⊙O的弦,OC是半径,OC⊥AB,AB=8,OD=3,则⊙O的半径为( )
如图,AB是⊙O的弦,OC是半径,OC⊥AB,AB=8,OD=3,则⊙O的半径为( )
 如图,AB是⊙O的弦,OC是半径,OC⊥AB,AB=8,OD=3,则⊙O的半径为( )
如图,AB是⊙O的弦,OC是半径,OC⊥AB,AB=8,OD=3,则⊙O的半径为( )| A. | 4 | B. | 5 | C. | 6 | D. | 8 |
18.下面两个电子数字成中心对称的是( )
| A. |  | B. |  | C. |  | D. |  |
15.已知ab=1,则$\frac{a}{a+1}+\frac{b}{b+1}$的值是( )
| A. | 0 | B. | -1 | C. | 1 | D. | 2 |

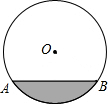 排水管的截面为如图所示的⊙O,半径为5m,如果圆心O到水面的距离是3m,那么水面宽AB=8m.
排水管的截面为如图所示的⊙O,半径为5m,如果圆心O到水面的距离是3m,那么水面宽AB=8m.