题目内容
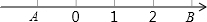 如图,在数轴上有A,B两点,A,B两点表示的有理数分别是a和b,a的倒数等于它本身,|b|=3,a<b且ab<0.
如图,在数轴上有A,B两点,A,B两点表示的有理数分别是a和b,a的倒数等于它本身,|b|=3,a<b且ab<0.(1)求线段AB的长;
(2)动点P,Q分别从点A,O同时出发,沿线段AB方向同向而行,其中一个点到达B点时停止,另一个点继续运动,直至也到达B点停止,P,Q的运动速度分别是2个单位/秒和一个单位/秒,M是PQ的中点,设运动时间为t秒,当点P.Q都在线段OB上运动时,请用含有t的式子表示线段OM的长;
(3)在(2)的条件下,是否存在t值使线段OM的长度是
| 7 |
| 4 |
考点:一元一次方程的应用,数轴
专题:
分析:(1)根据倒数的定义可知,±1的倒数等于它本身,|b|=3,b=±3,又因为a<b且ab<0,可得a=-1,b=3.
(2)先求出OP和OQ的长度分别为2t-1和t,得出OM的长为t+
(2t-1-t);
(3)列出方程t+
(2t-1-t)=
,解答即可.
(2)先求出OP和OQ的长度分别为2t-1和t,得出OM的长为t+
| 1 |
| 2 |
(3)列出方程t+
| 1 |
| 2 |
| 7 |
| 4 |
解答:解:(1)因为±1的倒数等于它本身,得a=±1,
因为|b|=3,b=±3,
又因为a<b且ab<0,
可得a=-1,b=3
所以线段AB的长=3+1=4;
(2)设运动时间为t秒,
因为P,Q的运动速度分别是2个单位/秒和一个单位/秒,
可得OP=2t-1,OQ=t;
又因为M是PQ的中点,
可得:OM的长为t+
(2t-1-t)=
t-
;
(3)因为线段OM的长度是
,可列出方程:
t-
=
,
解得:t=
.
故答案为:(1)4;(2)
t-
;(3)
秒.
因为|b|=3,b=±3,
又因为a<b且ab<0,
可得a=-1,b=3
所以线段AB的长=3+1=4;
(2)设运动时间为t秒,
因为P,Q的运动速度分别是2个单位/秒和一个单位/秒,
可得OP=2t-1,OQ=t;
又因为M是PQ的中点,
可得:OM的长为t+
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
(3)因为线段OM的长度是
| 7 |
| 4 |
| 3 |
| 2 |
| 1 |
| 2 |
| 7 |
| 4 |
解得:t=
| 3 |
| 2 |
故答案为:(1)4;(2)
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
点评:本题考查了一元一次方程的知识,第一问需要求出线段AB的距离,难点在第二问表示出OM的长度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
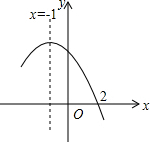 如图所示的是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是x=-1,有下列结论:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),(-4,y2)是抛物线上两点,则y1>y2,其中结论正确的序号是( )
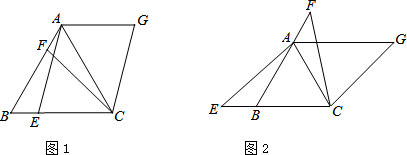
如图所示的是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是x=-1,有下列结论:①b-2a=0;②4a-2b+c<0;③a-b+c=-9a;④若(-3,y1),(-4,y2)是抛物线上两点,则y1>y2,其中结论正确的序号是( ) 如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交0F于点E.
如图,△ABC中,AB=AC,以AB为直径的⊙O分别交AC、BC于点D、F,连接BD交0F于点E.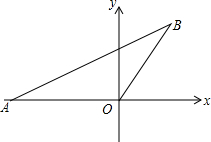 如图,OA=OB,点A的坐标是(-2,0),OB与x轴正方向夹角为60°,请画出过A,O,B三点的圆,写出圆心的坐标是
如图,OA=OB,点A的坐标是(-2,0),OB与x轴正方向夹角为60°,请画出过A,O,B三点的圆,写出圆心的坐标是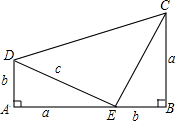 如图所示,△ADE≌△BEC,∠A=∠B=90°,A,D,B三点在一条直线上,借助这个图形,你能用面积法来验证勾股定理吗?
如图所示,△ADE≌△BEC,∠A=∠B=90°,A,D,B三点在一条直线上,借助这个图形,你能用面积法来验证勾股定理吗?