题目内容
14. 如图,AB是⊙O的直径,CD是弦,且CD⊥AB,垂足是P.如果CD=4,PB=1,那么直径AB=5.
如图,AB是⊙O的直径,CD是弦,且CD⊥AB,垂足是P.如果CD=4,PB=1,那么直径AB=5.
分析 连接OC,设OC=OB=r,由勾股定理得出关于r的方程,求出方程的解即可.
解答  解:连接OC,设OC=OB=r,
解:连接OC,设OC=OB=r,
则OP=r-1,
在Rt△OCP中,由勾股定理得:OC2=OP2+CP2,
∴r2=(r-1)2+22,
r=$\frac{5}{2}$,
∴AB=2r=5,
故答案为:5.
点评 本题考查了解一元一次方程,垂径定理,勾股定理等知识点的应用,解此题的关键是构造直角三角形后得出关于r的方程,用的数学思想是方程思想,是一道比较典型的题目,难度也不大.

练习册系列答案
相关题目
4.可用来表示13的立方根的是( )
| A. | $\sqrt{13}$ | B. | $\root{3}{13}$ | C. | ±$\sqrt{13}$ | D. | ±$\root{3}{13}$ |
9.在一定限度内,每悬挂一定质量的物体,弹簧就会相应拉长一段长度,有一种弹簧的长度(cm)与所悬挂物体的质量(kg)之间的关系如下表所示:
(1)悬挂质量为x(kg)的物体后弹簧的长度为(8+0.6x)cm.
(2)若悬挂物体后弹簧的长度为17cm,求该物体的质量.
| 悬挂物体的质量(kg) | 0 | 1 | 2 | 3 | 4 | … |
| 弹簧的长度(cm) | 8 | 8.6 | 9.2 | 9.8 | 10.4 | … |
(2)若悬挂物体后弹簧的长度为17cm,求该物体的质量.
 如图,利用网格线画出图中∠ACB的平分线和线段BC的垂直平分线,设两条线的交点为P,试说明与点P有关的正确结论.
如图,利用网格线画出图中∠ACB的平分线和线段BC的垂直平分线,设两条线的交点为P,试说明与点P有关的正确结论. 已知,一次函数y=kx+b的图象与二次函数y=ax2的图象交于点A(1,m)和B(-2,4),与y轴交于点C.
已知,一次函数y=kx+b的图象与二次函数y=ax2的图象交于点A(1,m)和B(-2,4),与y轴交于点C.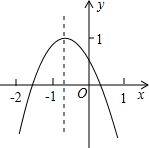 二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b+c,N=a-c,P=-$\frac{b}{2a}$,则在M,N,P中,值小于0的数有( )
二次函数y=ax2+bx+c(a≠0)的图象如图所示,若M=a+b+c,N=a-c,P=-$\frac{b}{2a}$,则在M,N,P中,值小于0的数有( )