题目内容
如图,在锐角三角形ABC中,BC=12,△ABC的面积为48,D,E分别是边AB,AC上的两个动点(D不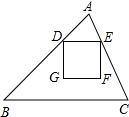 与A,B重合),且保持DE∥BC,以DE为边,在点A的异侧作正方形DEFG.
与A,B重合),且保持DE∥BC,以DE为边,在点A的异侧作正方形DEFG.(1)当正方形DEFG的边GF在BC上时,求正方形DEFG的边长;
(2)设DE=x,△ABC与正方形DEFG重叠部分的面积为y,试求y关于x的函数关系式,写出x的取值范围,并求出y的最大值.
分析:(1)根据题意,作出图示;分析可得:AM=8,且△ADE∽△ABC,进而可得
=
,解可得答案.
(2)分两种情况:①当正方形DEFG在△ABC的内部时,②当正方形DEFG的一部分在△ABC的外部时,依据平行线以及正方形的性质,可得二次函数,再根据二次函数的性质,解可得重合部分的面积,比较可得面积的最大值.
| DE |
| 12 |
| 8-DE |
| 8 |
(2)分两种情况:①当正方形DEFG在△ABC的内部时,②当正方形DEFG的一部分在△ABC的外部时,依据平行线以及正方形的性质,可得二次函数,再根据二次函数的性质,解可得重合部分的面积,比较可得面积的最大值.
解答:解:
(1)当正方形DEFG的边GF在BC上时,如图(1),过点A作BC边上的高AM,交DE于N,垂足为M.
∵S△ABC=48,BC=12,∴AM=8,
∵DE∥BC,△ADE∽△ABC,
∴
=
,
而AN=AM-MN=AM-DE,∴
=
,
解之得DE=4.8.∴当正方形DEFG的边GF在BC上时,正方形DEFG的边长为4.8,

(2)分两种情况:
①当正方形DEFG在△ABC的内部时,
如图(2),△ABC与正方形DEFG重叠部分的面积为正方形DEFG的面积,
∵DE=x,∴y=x2,
此时x的范围是0<x≤4.8,
②当正方形DEFG的一部分在△ABC的外部时,
如图(3),设DG与BC交于点Q,EF与BC交于点P,
△ABC的高AM交DE于N,
∵DE=x,DE∥BC,∴△ADE∽△ABC,
即
=
,而AN=AM-MN=AM-EP,
∴
=
,解得EP=8-
x.
所以y=x(8-
x),即y=-
x2+8x,
由题意,x>4.8,且x<12,所以4.8<x<12;
因此△ABC与正方形DEFG重叠部分的面积需分两种情况讨论,
当0<x≤4.8时,△ABC与正方形DEFG重叠部分的面积的最大值为4.82=23.04,
当4.8<x<12时,因为y=-
x2+8x,
所以当x=-
=6时,
△ABC与正方形DEFG重叠部分的面积的最大值为二次函数的最大值:y最大=-
×62+8×6=24;
因为24>23.04,
所以△ABC与正方形DEFG重叠部分的面积的最大值为24.
(1)当正方形DEFG的边GF在BC上时,如图(1),过点A作BC边上的高AM,交DE于N,垂足为M.
∵S△ABC=48,BC=12,∴AM=8,
∵DE∥BC,△ADE∽△ABC,
∴
| DE |
| BC |
| AN |
| AM |
而AN=AM-MN=AM-DE,∴
| DE |
| 12 |
| 8-DE |
| 8 |
解之得DE=4.8.∴当正方形DEFG的边GF在BC上时,正方形DEFG的边长为4.8,

(2)分两种情况:
①当正方形DEFG在△ABC的内部时,
如图(2),△ABC与正方形DEFG重叠部分的面积为正方形DEFG的面积,
∵DE=x,∴y=x2,
此时x的范围是0<x≤4.8,
②当正方形DEFG的一部分在△ABC的外部时,
如图(3),设DG与BC交于点Q,EF与BC交于点P,
△ABC的高AM交DE于N,
∵DE=x,DE∥BC,∴△ADE∽△ABC,
即
| DE |
| BC |
| AN |
| AM |
∴
| x |
| 12 |
| 8-EP |
| 8 |
| 2 |
| 3 |
所以y=x(8-
| 2 |
| 3 |
| 2 |
| 3 |
由题意,x>4.8,且x<12,所以4.8<x<12;
因此△ABC与正方形DEFG重叠部分的面积需分两种情况讨论,
当0<x≤4.8时,△ABC与正方形DEFG重叠部分的面积的最大值为4.82=23.04,
当4.8<x<12时,因为y=-
| 2 |
| 3 |
所以当x=-
| 8 | ||
2×(-
|
△ABC与正方形DEFG重叠部分的面积的最大值为二次函数的最大值:y最大=-
| 2 |
| 3 |
因为24>23.04,
所以△ABC与正方形DEFG重叠部分的面积的最大值为24.
点评:本题主要考查了二次函数,平行线以及正方形的性质等知识点,要根据题意,得到二次函数关系,再根据二次函数的性质,即可得答案.

练习册系列答案
相关题目
 如图,在锐角三角形ABC中,AD⊥BC,AD=12cm,AB=13cm,BC=14cm,则AC的长为( )
如图,在锐角三角形ABC中,AD⊥BC,AD=12cm,AB=13cm,BC=14cm,则AC的长为( )| A、12cm | B、13cm | C、14cm | D、15cm |
 (1)如图,在锐角三角形ABC中,BC=12,
(1)如图,在锐角三角形ABC中,BC=12, 如图,在锐角三角形ABC中,AD⊥BC,AD=12,AC=13,BC=14.则AB=
如图,在锐角三角形ABC中,AD⊥BC,AD=12,AC=13,BC=14.则AB= 如图,在锐角三角形ABC中,AD、CE分别是边BC、AB上的高,垂足分别是D、E,AD、CE相交于点O,若∠B=60°,则∠AOE的度数是( )
如图,在锐角三角形ABC中,AD、CE分别是边BC、AB上的高,垂足分别是D、E,AD、CE相交于点O,若∠B=60°,则∠AOE的度数是( ) 如图,在锐角三角形ABC中,BC=
如图,在锐角三角形ABC中,BC=