题目内容
9.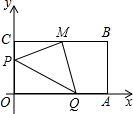 探究:如图.已知矩形OABC,顶点A、C分别在x、y 轴的正半轴上,点B的坐标为(8,4),M是BC的中点.动点P、Q同时从点O出发.分别沿线段OC和OA向点C和点A运动(任一点到达目的后两动点同时停止运动).点P的速度为1个单位/秒,点Q的速度为2个单位/秒.设运动的时间为t秒.求当t为何值时,△MPQ的面积为5平方单位?
探究:如图.已知矩形OABC,顶点A、C分别在x、y 轴的正半轴上,点B的坐标为(8,4),M是BC的中点.动点P、Q同时从点O出发.分别沿线段OC和OA向点C和点A运动(任一点到达目的后两动点同时停止运动).点P的速度为1个单位/秒,点Q的速度为2个单位/秒.设运动的时间为t秒.求当t为何值时,△MPQ的面积为5平方单位?
分析 根据已知表示出PC,PO,QO,AQ的长,进而利用矩形面积减去周围三角形和梯形面积,得出等式求出答案即可.
解答 解:设t秒时,△MPQ的面积为5平方单位,
由题意可得:PC=4-t,PO=t,QO=2t,AQ=8-2t,BM=CM=4,AB=4,
故S△PMQ=S矩形ABCO-S△OPQ-S△PCM-S梯形AQBM
5=4×8-$\frac{1}{2}$t•2t-$\frac{1}{2}$(4-t)•4-$\frac{1}{2}$(4+8-2t)×4
整理得:t2-6t+5=0,
解得:t1=1,t2=5(不合题意舍去),
答:当t为1秒时,△MPQ的面积为5平方单位.
点评 此题主要考查了一元二次方程的应用,根据题意表示出各线段长是解题关键.

练习册系列答案
 学业测评一课一测系列答案
学业测评一课一测系列答案 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案
相关题目
20.下列方程中,是一元一次方程的是( )
| A. | 3x+y=5 | B. | y2=1 | C. | $\frac{1}{x}$=3 | D. | 3x+2=4x-7 |
18. 如图,CD为⊙O的直径,CD⊥EF,垂点为G,∠EOD=40°,则∠DCF=( )
如图,CD为⊙O的直径,CD⊥EF,垂点为G,∠EOD=40°,则∠DCF=( )
 如图,CD为⊙O的直径,CD⊥EF,垂点为G,∠EOD=40°,则∠DCF=( )
如图,CD为⊙O的直径,CD⊥EF,垂点为G,∠EOD=40°,则∠DCF=( )| A. | 80° | B. | 50° | C. | 40° | D. | 20° |
19.能判定△ABC和△A′B′C′相似的条件是( )
| A. | $\frac{AB}{A'B'}=\frac{AC}{A'C'}$ | B. | $\frac{AB}{AC}=\frac{A'B'}{A'C'}$且∠A=∠C′ | ||
| C. | $\frac{AB}{A'B'}=\frac{BC}{A'C'}$且∠B=∠A′ | D. | $\frac{AB}{A'B'}=\frac{AC}{A'C'}$且∠B=∠B′ |
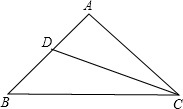 如图,△ABC中,∠A=90°,CD平分∠ACB,若AD=1,AC=2,BC=$\frac{10}{3}$,求△ABC的面积.
如图,△ABC中,∠A=90°,CD平分∠ACB,若AD=1,AC=2,BC=$\frac{10}{3}$,求△ABC的面积.