题目内容
3.关于x的一元二次方程ax2+bx+c=0(a≠0)的一个根为x=1,且a,b满足|a-2|+(b+1)2=0,求方程$\frac{1}{4}$y2+c=0的两根.分析 根据一元二次方程ax2+bx+c=0的一个根为x=1,得a+b+c=0,再由a,b满足|a-2|+(b+1)2=0,得a=2,b=-1,得出c代入方程$\frac{1}{4}$y2+c=0,求得根即可.
解答 解:∵一元二次方程ax2+bx+c=0的一个根为x=1,
∴a+b+c=0,
∵a,b满足|a-2|+(b+1)2=0,
∴a=2,b=-1,
则c=-a-b=-2+1=-1,
故$\frac{1}{4}$y2-1=0,
解得y1=2,y2=-2.
点评 本题考查了一元二次方程的解和非负数的性质.能使一元二次方程左右两边相等的未知数的值是一元二次方程的解.又因为只含有一个未知数的方程的解也叫做这个方程的根,所以,一元二次方程的解也称为一元二次方程的根.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.某股票经纪人给他的投资者列出下表,说明投资人的盈利净赚情况:(单位:元)
请你计算一下,投资者到底赔了还是赚了?赔或赚了多少元?
| 股票名称 | 每股净赚(元) | 股数 |
| 天河 | +4 | 500 |
| 北斗 | -1.5 | 1000 |
| 白马 | +3 | 1000 |
| 海潮 | -2 | 500 |
15.下列说法正确的是( )
| A. | 23x5的系数是1,次数是8 | B. | 若x2+mx是单项式,则m=0 | ||
| C. | 若-$\frac{2}{3}$xmy3的次数是5,则m=5 | D. | 0不是单项式 |
8.下列函数中,y随x的增大而减小的有( )
| A. | y=-x | B. | y=2+3x | C. | y=5x | D. | y=-3+2x |
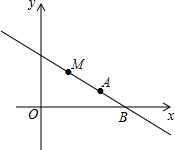 如图,一次函数y=kx+3(k≠0)的图象经过点A(4,1),与x轴相交于点B,直线上有一点M(a,b),且a+b=4.
如图,一次函数y=kx+3(k≠0)的图象经过点A(4,1),与x轴相交于点B,直线上有一点M(a,b),且a+b=4.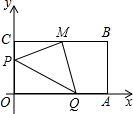 探究:如图.已知矩形OABC,顶点A、C分别在x、y 轴的正半轴上,点B的坐标为(8,4),M是BC的中点.动点P、Q同时从点O出发.分别沿线段OC和OA向点C和点A运动(任一点到达目的后两动点同时停止运动).点P的速度为1个单位/秒,点Q的速度为2个单位/秒.设运动的时间为t秒.求当t为何值时,△MPQ的面积为5平方单位?
探究:如图.已知矩形OABC,顶点A、C分别在x、y 轴的正半轴上,点B的坐标为(8,4),M是BC的中点.动点P、Q同时从点O出发.分别沿线段OC和OA向点C和点A运动(任一点到达目的后两动点同时停止运动).点P的速度为1个单位/秒,点Q的速度为2个单位/秒.设运动的时间为t秒.求当t为何值时,△MPQ的面积为5平方单位?