题目内容
20.已知关于x的方程(x-1)(x-2)-p=0.(1)如果方程有两个不相等的实数根,求P的取值范围;
(2)设方程两个不相等的实数根分别为x1,x2,且满足x1、x2,且满足x1+x2=$\frac{{x}_{1}^{2}{x}_{2}^{2}}{3}$,求实数p的值.
分析 (1)先把方程(x-1)(x-2)-p=0化为x2-3x+2-p=0,再根据方程有两个不相等的实数根可得△=9-8+4p>0,解不等式求出p的取值范围;
(2)由根与系数的关系可得x1+x2=3,x1•x2=2-p,代入x1+x2=$\frac{{x}_{1}^{2}{x}_{2}^{2}}{3}$,得到关于p的方程,结合k的取值范围解方程即可.
解答 解:(1)方程(x-1)(x-2)-p=0可化为x2-3x+2-p=0,
这里a=1,b=-3,c=2-p,
∵方程有两个不相等的实数根,
∴△=b2-4ac=(-3)2-4×1×(2-p)=9-8+4p>0,
∴p>-$\frac{1}{4}$,即满足条件的p的取值范围为p>-$\frac{1}{4}$;
(2)由题意可得:x1+x2=3,x1x2=2-p,
又∵x1+x2=$\frac{{x}_{1}^{2}{x}_{2}^{2}}{3}$,
∴3=$\frac{(2-p)^{2}}{3}$,
∴(2-p)2=9,
∴p1=5,p2=-1,
∵p>-$\frac{1}{4}$,
∴取p=5,即满足条件的p的值为5.
点评 本题考查了根与系数的关系:若x1,x2是一元二次方程ax2+bx+c=0(a≠0)的两根时,x1+x2=-$\frac{b}{a}$,x1x2=$\frac{c}{a}$.也考查了根的判别式.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
10.《九章算术》中“今有勾七步,股有二十四步,问勾中容圆径几何?”其意思是:“今有直角三角形,勾(短直角边)长为7步,股(长直角边)长为24步,问该直角三角形的容圆(内切圆)直径是多少?”( )
| A. | 4步 | B. | 5步 | C. | 6步 | D. | 8步 |
15.下列运算正确的是( )
| A. | x3+x4=x7 | B. | 2x3•x2=2x6 | C. | (3x3)2=9x6 | D. | x6÷x3=x2 |
12. 将全体自然数排列成如图所示的三角形数阵,根据排列规律,则数阵中,第10行第6个数是( )
将全体自然数排列成如图所示的三角形数阵,根据排列规律,则数阵中,第10行第6个数是( )
 将全体自然数排列成如图所示的三角形数阵,根据排列规律,则数阵中,第10行第6个数是( )
将全体自然数排列成如图所示的三角形数阵,根据排列规律,则数阵中,第10行第6个数是( )| A. | 49 | B. | 50 | C. | 52 | D. | 48 |
9.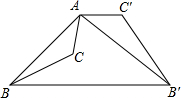 如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转100°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转100°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
 如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转100°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )
如图,已知钝角三角形ABC,将△ABC绕点A按逆时针方向旋转100°得到△AB′C′,连接BB′,若AC′∥BB′,则∠CAB′的度数为( )| A. | 50° | B. | 60° | C. | 70° | D. | 80° |
10.某公司开发两种新产品,A型产品600件,B型产品400件,分配到甲、乙两地试销,其中甲地销售700件,乙地销售300件,两地销售这两种产品每件的利润(元)如表
设分配到甲地A型产品x件,公司售完这1000件产品的总利润为W(元)
(1)求W关于x的函数关系式,并求出最大利润是多少?
(2)为了加快A型产品的销售,公司决定对A型产品加强广告宣传,由于销售成本增加,A型产品的每件销售利润有所降低,甲地的每件销售利润降低$\frac{x}{100}$元,乙地的每件销售利润降低2元,那么公司售完这1000件产品最小可以获得多少利润?
| A型利润 | B型利润 | |
| 甲地 | 20 | 17 |
| 乙地 | 16 | 15 |
(1)求W关于x的函数关系式,并求出最大利润是多少?
(2)为了加快A型产品的销售,公司决定对A型产品加强广告宣传,由于销售成本增加,A型产品的每件销售利润有所降低,甲地的每件销售利润降低$\frac{x}{100}$元,乙地的每件销售利润降低2元,那么公司售完这1000件产品最小可以获得多少利润?