题目内容
13. 已知:如图,将∠ABC放置在正方形网格纸中,其中点A、B、C均在格点上,则tan∠ABC的值是( )
已知:如图,将∠ABC放置在正方形网格纸中,其中点A、B、C均在格点上,则tan∠ABC的值是( )| A. | 2 | B. | $\frac{1}{2}$ | C. | $\frac{{\sqrt{5}}}{2}$ | D. | $\frac{{2\sqrt{5}}}{5}$ |
分析 在直角三角形ABC中,利用锐角三角函数定义求出tan∠ABC的值即可.
解答 解:在Rt△ABC中,AC=4,BC=2,
则tan∠ABC=$\frac{AC}{BC}$=$\frac{4}{2}$=2,
故选A
点评 此题考查了锐角三角函数的定义,熟练掌握锐角三角函数的定义是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
1. 如图,OD平分∠AOB,过点D作CD∥OB交OA于C,若∠D=36°,则∠ACD=( )
如图,OD平分∠AOB,过点D作CD∥OB交OA于C,若∠D=36°,则∠ACD=( )
 如图,OD平分∠AOB,过点D作CD∥OB交OA于C,若∠D=36°,则∠ACD=( )
如图,OD平分∠AOB,过点D作CD∥OB交OA于C,若∠D=36°,则∠ACD=( )| A. | 54° | B. | 60° | C. | 63° | D. | 72° |
5. 如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(1,$\sqrt{3}$),将线段OA绕原点O逆时针旋转30°,得到线段OB,则点B的坐标是( )
如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(1,$\sqrt{3}$),将线段OA绕原点O逆时针旋转30°,得到线段OB,则点B的坐标是( )
 如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(1,$\sqrt{3}$),将线段OA绕原点O逆时针旋转30°,得到线段OB,则点B的坐标是( )
如图,在平面直角坐标系中,O为坐标原点,点A的坐标为(1,$\sqrt{3}$),将线段OA绕原点O逆时针旋转30°,得到线段OB,则点B的坐标是( )| A. | (0,2) | B. | (2,0) | C. | (1,-$\sqrt{3}$) | D. | (-1,$\sqrt{3}$) |
1.两根木棒分别为5cm和7cm,要选择第三根,将它们钉成一个三角形,如果第三根木棒长为偶数,则方法有( )
| A. | 3种 | B. | 4种 | C. | 5种 | D. | 6种 |

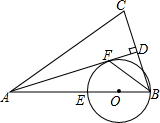 如图,在△ABC中,AB=AC,AD是BC边上的高线,BF平分∠ABC交AD于点F,以AB上的点O为圆心,OB为半径的⊙O交AB于点E,恰好经过点F.
如图,在△ABC中,AB=AC,AD是BC边上的高线,BF平分∠ABC交AD于点F,以AB上的点O为圆心,OB为半径的⊙O交AB于点E,恰好经过点F.