题目内容
7.近年来,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车行经营的A型车去年3月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年3月份与去年3月份卖出的A型车数量相同,则今年3月份A型车销售总额将比去年3月份销售总额增加25%.(1)求今年3月份A型车每辆销售价多少元;
(2)该车行计划4月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格表:
| A型车 | B型车 | |
| 进货价格(元/辆) | 1100 | 1400 |
| 销售价格(元/辆) | 今年的销售价格 | 2400 |
分析 (1)设去年3月份A型车每辆销售价x元,那么今年3月份每辆(x+400)元,列出方程即可解决问题.
(2)设今年4月份进A型车m辆,则B型车(50-m)辆,获得的总利润为y元,先求出m的范围,构建一次函数,利用函数性质解决问题.
解答 解:(1)设去年3月份A型车每辆销售价x元,那么今年3月份每辆(x+400)元,
根据题意得$\frac{32000}{x}$=$\frac{32000(1+25%)}{x+400}$,
解之得x=1600,
经检验,x=1600是方程的解.
x=1600时,x+400═2000.
答:今年A型车每辆2000元.
(2)设今年4月份进A型车m辆,则B型车(50-m)辆,获得的总利润为y元,
根据题意得50-m≤2m,
解之得m≥16$\frac{2}{3}$,
∵y=(2000-1100)m+(2400-1400)(50-m)=-100m+50000,
∴y随m 的增大而减小,
∴当m=17时,可以获得最大利润.
答:进货方案是A型车17辆,B型车33辆.
点评 本题考查一次函数的应用、分式方程等知识,解题的关键是设未知数列出方程解决问题,注意分式方程必须检验,学会构建一次函数,利用一次函数性质解决实际问题中的最值问题,属于中考常考题型.

练习册系列答案
相关题目
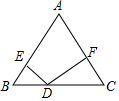 如图,在等腰三角形△ABC中,AB=AC=5,BC=6,D为底边BC上一动点(不与B、C重合)DE⊥AB,DF⊥AC,垂足分别为E、F,则DE+DF=$\frac{24}{5}$.
如图,在等腰三角形△ABC中,AB=AC=5,BC=6,D为底边BC上一动点(不与B、C重合)DE⊥AB,DF⊥AC,垂足分别为E、F,则DE+DF=$\frac{24}{5}$.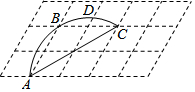 如图,15个形状大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角为60°,A、B、C都在格点上,点D在过A、B、C三点的圆弧上,若E也在格点上,且∠AED=∠ACD,则cos∠AEC=$\frac{1}{2}$.
如图,15个形状大小完全相同的菱形组成网格,菱形的顶点称为格点.已知菱形的一个角为60°,A、B、C都在格点上,点D在过A、B、C三点的圆弧上,若E也在格点上,且∠AED=∠ACD,则cos∠AEC=$\frac{1}{2}$.