题目内容
18.若干张长方形和正方形卡片如图所示.(1)选取1张①号卡片、4张②号卡片、4张③号卡片,请你拼出一个正方形.给出理由并画出图形.
(2)若已选取2张①号卡片、1张②号卡片,则还需要几张③号卡片才能拼出一个长方形?给出理由并画出图形.
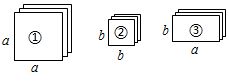
分析 (1)利用完全平方公式求出拼成后的正方形的面积,然后分解因式即可得出所画正方形的边长,根据边长画图形即可;
(2)猜想长方形的边长,计算的面积与拼成后的面积相等.
解答 解:(1)∵a2+4ab+4b2=(a+2b)2,
∴拼成一个边长为a+2b的正方形,如图1所示:
(2)∵(2a+b)(a+b)=2a2+3ab+b2;
∴则还需要3张③号卡片才能拼出一个长方形,如图2所示:
点评 本题考查了完全平方公式及多项式乘以多项式,立意较新颖,注意对此类问题的深入理解,本题只要读懂题意,然后根据各图形的面积即可找出其中的关系.

练习册系列答案
相关题目
6.下列说法中错误的是( )
| A. | 等腰三角形至少有两个角相等 | |
| B. | 等腰三角形的底角一定是锐角 | |
| C. | 等腰三角形顶角的外角是底角的2倍 | |
| D. | 等腰三角形中有一个角是45°,那它一定是等腰直角三角形 |
7.近年来,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车行经营的A型车去年3月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年3月份与去年3月份卖出的A型车数量相同,则今年3月份A型车销售总额将比去年3月份销售总额增加25%.
(1)求今年3月份A型车每辆销售价多少元;
(2)该车行计划4月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格表:
(1)求今年3月份A型车每辆销售价多少元;
(2)该车行计划4月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格表:
| A型车 | B型车 | |
| 进货价格(元/辆) | 1100 | 1400 |
| 销售价格(元/辆) | 今年的销售价格 | 2400 |
8.问题提出:用水平线和竖直线将平面分成若干个面积为1的小长方形格子,小长方形的顶点叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x,多边形内部的格点数为n,S与x,n之间是否存在一定的数量关系呢?
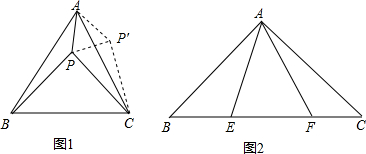
问题探究:(1)如图1,图中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式S=$\frac{1}{2}$x.
(2)在图2中所示的格点多边形,这些多边形内部都有且只有2个格点.探究此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S=$\frac{1}{2}$x+1.
(3)请继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x,n之间的关系式S=$\frac{1}{2}$x+(n-1)(用含有字母x,n的代数式表示)
问题拓展:请在正三角形网格中的类似问题进行探究:在图3、4中正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,图是该正三角形格点中的两个多边形.
根据图中提供的信息填表:
则S与a,b之间的关系为S=a+2b-2(用含a,b的代数式表示).

问题探究:(1)如图1,图中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式S=$\frac{1}{2}$x.
| 多边形的序号 | ① | ② | ③ | ④ | … |
| 多边形的面积S | 2 | 2.5 | 3 | 4 | … |
| 各边上格点的个数和x | 4 | 5 | 6 | 8 | … |
(3)请继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x,n之间的关系式S=$\frac{1}{2}$x+(n-1)(用含有字母x,n的代数式表示)
问题拓展:请在正三角形网格中的类似问题进行探究:在图3、4中正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,图是该正三角形格点中的两个多边形.
根据图中提供的信息填表:
| 格点多边形各边上的格点的个数 | 格点多边形内部的格点个数 | 格点多边形的面积 | |
| 多边形1(图3) | 8 | 1 | 8 |
| 多边形2(图4) | 7 | 3 | 11 |
| … | … | … | … |
| … | … | … | … |
| … | … | … | … |
| 一般格点多边形 | a | b | S |
 如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B,点C(5,m)在抛物线上,直线BC交x轴于点E.
如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B,点C(5,m)在抛物线上,直线BC交x轴于点E.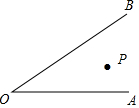 如图,点P在∠AOB内.
如图,点P在∠AOB内.