题目内容
12.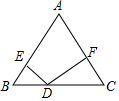 如图,在等腰三角形△ABC中,AB=AC=5,BC=6,D为底边BC上一动点(不与B、C重合)DE⊥AB,DF⊥AC,垂足分别为E、F,则DE+DF=$\frac{24}{5}$.
如图,在等腰三角形△ABC中,AB=AC=5,BC=6,D为底边BC上一动点(不与B、C重合)DE⊥AB,DF⊥AC,垂足分别为E、F,则DE+DF=$\frac{24}{5}$.
分析 如图连接AD,作AH⊥BC于H.首先利用勾股定理求出AH,再根据S△ABC=S△ABD+S△ACD,DE⊥AB,DF⊥AC,可得$\frac{1}{2}$•BC•AH=$\frac{1}{2}$•AB•DE+$\frac{1}{2}$•AC•DF,由此即可解决问题.
解答 解:如图连接AD,作AH⊥BC于H.
∵AB=AC=5,AH⊥BC,
∴BH=CH=3,
在Rt△ABH中,AH=$\sqrt{A{B}^{2}-B{H}^{2}}$=$\sqrt{{5}^{2}-{3}^{2}}$=4,
∵S△ABC=S△ABD+S△ACD,DE⊥AB,DF⊥AC,
∴$\frac{1}{2}$•BC•AH=$\frac{1}{2}$•AB•DE+$\frac{1}{2}$•AC•DF,
∴6×4=5DE+5DF,
∴DE+DF=$\frac{24}{5}$,
故答案为$\frac{24}{5}$.
点评 本题考查等腰三角形的性质,勾股定理,三角形的面积等知识,解题的关键是学会利用面积法解决问题,属于中考常考题型.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.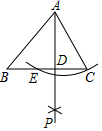 如图,已知锐角三角形ABC,以点A为圆心,AC为半径画弧与BC交于点E,分别以点E、C为圆心,以大于$\frac{1}{2}$EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=$\frac{3}{4}$,则AC的长为( )
如图,已知锐角三角形ABC,以点A为圆心,AC为半径画弧与BC交于点E,分别以点E、C为圆心,以大于$\frac{1}{2}$EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=$\frac{3}{4}$,则AC的长为( )
 如图,已知锐角三角形ABC,以点A为圆心,AC为半径画弧与BC交于点E,分别以点E、C为圆心,以大于$\frac{1}{2}$EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=$\frac{3}{4}$,则AC的长为( )
如图,已知锐角三角形ABC,以点A为圆心,AC为半径画弧与BC交于点E,分别以点E、C为圆心,以大于$\frac{1}{2}$EC的长为半径画弧相交于点P,作射线AP,交BC于点D.若BC=5,AD=4,tan∠BAD=$\frac{3}{4}$,则AC的长为( )| A. | 3 | B. | 5 | C. | $\sqrt{5}$ | D. | 2$\sqrt{5}$ |
7.近年来,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场,顺风车行经营的A型车去年3月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年3月份与去年3月份卖出的A型车数量相同,则今年3月份A型车销售总额将比去年3月份销售总额增加25%.
(1)求今年3月份A型车每辆销售价多少元;
(2)该车行计划4月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格表:
(1)求今年3月份A型车每辆销售价多少元;
(2)该车行计划4月份新进一批A型车和B型车共50辆,且B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最多?
A,B两种型号车的进货和销售价格表:
| A型车 | B型车 | |
| 进货价格(元/辆) | 1100 | 1400 |
| 销售价格(元/辆) | 今年的销售价格 | 2400 |
17.某中学去年通过“废品回收”活动筹集资金用于资助贫困山区中、小学生共27名,其中资助一名中学生的学习费用需要x元,资助一名小学生的学习费用需要y元,各年级学生筹集资金的数额及用其恰好资助中、小学生人数的部分情况如下表:
(1)求x,y的值;
(2)九年级学生筹集的资金数解决了其余贫困中、小学生的学习费用,求出九年级学生资助的贫困中、小学生人数.
| 年级 | 筹集资金数额 | 资助贫困中学 | 资助贫困小学生人数(名) |
| 七年级 | 5000 | 2 | 5 |
| 八年级 | 6000 | 3 | 5 |
| 九年级 | 8000 |
(2)九年级学生筹集的资金数解决了其余贫困中、小学生的学习费用,求出九年级学生资助的贫困中、小学生人数.
2.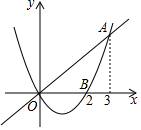 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )
 如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )
如图,已知二次函数y1=$\frac{2}{3}$x2-$\frac{4}{3}$x的图象与正比例函数y2=$\frac{2}{3}$x的图象交于点A(3,2),与x轴交于点B(2,0),若y1<y2,则x的取值范围是( )| A. | 0<x<2 | B. | x<0或x>3 | C. | 2<x<3 | D. | 0<x<3 |
 如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B,点C(5,m)在抛物线上,直线BC交x轴于点E.
如图,已知抛物线y=ax2-x+c的对称轴为直线x=1,与x轴的一个交点为A(-1,0),顶点为B,点C(5,m)在抛物线上,直线BC交x轴于点E. 已知:如图,四边形ABCD中,AB⊥BC,AB=2,BC=4,CD=4,AD=6,求四边形ABCD的面积.
已知:如图,四边形ABCD中,AB⊥BC,AB=2,BC=4,CD=4,AD=6,求四边形ABCD的面积. 如图是某校参加各兴趣小组的学生人数分布扇形统计图,其中“演艺”兴趣小组一项所对应的角度是108°.
如图是某校参加各兴趣小组的学生人数分布扇形统计图,其中“演艺”兴趣小组一项所对应的角度是108°.