Question

19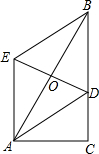．如图，在Rt△ABC中，∠C=90°，AB=2$\sqrt{3}$，BC=3，点D在BC上，以AB为对角线的所有?ADBE中，对角线DE最小的值是（　　）

• A． 3
• B． 6
• C． $\sqrt{3}$
• D． 2$\sqrt{3}$

Answer 1

分析 由平行四边形的对角线互相平分、垂线段最短知，当OD⊥AC时，DE线段取最小值．

解答 解：∵在Rt△ABC中，∠B=90°，
∴BC⊥AB．AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{3}$，
∵四边形ADBE是平行四边形，
∴OD=OE，OA=OB．
∴当OD取最小值时，DE线段最短，此时OD⊥BC．
∴OD∥AC．
又点O是AB的中点，
∴OD是△ABC的中位线，
∴OD=$\frac{1}{2}$AC=$\frac{\sqrt{3}}{2}$，
∴ED=2OD=$\sqrt{3}$．
故选C．

点评 本题考查了平行四边形的性质、三角形中位线定理、勾股定理以及垂线段最短．熟练掌握平行四边形的性质．求出OD的长是解决问题的关键．