题目内容
2.已知abc=1,求$\frac{1}{ab+a+1}$+$\frac{1}{bc+b+1}$+$\frac{1}{ca+c+1}$的值.分析 由abc=1,代入所求分式进行化简即可得出答案.
解答 解:∵abc=1
∴原式=$\frac{c}{c(ab+a+1)}+\frac{ac}{ac(bc+b+1)}+\frac{1}{ca+c+1}$
=$\frac{c}{abc+ac+c}$+$\frac{ac}{abc•c+abc+ac}$+$\frac{1}{ac+c+1}$
=$\frac{c}{ac+c+1}$+$\frac{ac}{ac+c+1}$+$\frac{1}{ac+c+1}$
=$\frac{ac+c+1}{ac+c+1}$
=1
点评 本题考查了分式的化简求值,难度不大,关键是条件abc=1的灵活运用.

练习册系列答案
相关题目
17.通过估算比较大小,下列结论不正确的是( )
| A. | $\root{3}{69}$$>\sqrt{16}$ | B. | -$\sqrt{10}$>$\root{3}{-27}$ | C. | $\frac{\sqrt{7}-2}{2}<\frac{1}{2}$ | D. | $\sqrt{15}<2\sqrt{5}$ |
2.生物兴趣小组的学生,将自己收集的标本向本组其他成员各赠送一件,全组共互赠了182件.如果全组共有x名同学,则根据题意列出的方程是( )
| A. | x(x+1)=182 | B. | x(x+1)=182×$\frac{1}{2}$ | C. | x(x-1)=182 | D. | x(x-1)=182×2 |
12. 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC的值为( )
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC的值为( )
 如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC的值为( )
如图,在半径为5cm的⊙O中,弦AB=6cm,OC⊥AB于点C,则OC的值为( )| A. | 6cm | B. | 5cm | C. | 4cm | D. | 3cm |
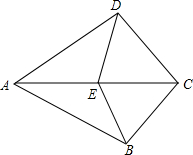 已知:∠ABC=∠ADC=90°,E是AC中点.
已知:∠ABC=∠ADC=90°,E是AC中点. 如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连结AE、AF、EF.
如图,已知四边形ABCD是正方形,E、F分别是DC和CB的延长线上的点,且DE=BF,连结AE、AF、EF. ∠AOB的大小可由量角器测得(如图所示),则∠AOB的补角的大小为120°.
∠AOB的大小可由量角器测得(如图所示),则∠AOB的补角的大小为120°.