题目内容
15.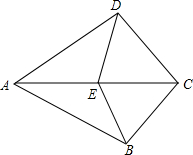 已知:∠ABC=∠ADC=90°,E是AC中点.
已知:∠ABC=∠ADC=90°,E是AC中点.(1)求证:ED=EB;
(2)图中有哪些等腰三角形?
分析 (1)根据直角三角形斜边上的中线等于斜边的一半即可证得EB=$\frac{1}{2}$AC,ED=$\frac{1}{2}$AC,据此即可证得;
(2)根据直角三角形斜边上的中线等于斜边的一半即可解答.
解答 (1)证明:∵∠ABC=90°,E是AC的中点,
∴EB=$\frac{1}{2}$AC,
同理,ED=$\frac{1}{2}$AC,
∴ED=EB;
(2)解:等腰三角形有:△ADE,△CDE,△ABE和△BCE.
点评 本题考查了直角三角形的性质,直角三角形斜边上的中线等于斜边的一半,理解定理是本题的关键.

练习册系列答案
相关题目
5.下列运算正确的是( )
| A. | ab2+a2b=2a2b2 | B. | -3ab+ab=-4ab | C. | a2-a=a | D. | m2n-nm2=0 |
10. 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
①a、b同号;
②当x=1和x=3时,函数值相等;
③4a+b=0;
④当-1<x<5时,y<0.
其中正确的有( )
 已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:
已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①a、b同号;
②当x=1和x=3时,函数值相等;
③4a+b=0;
④当-1<x<5时,y<0.
其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
19.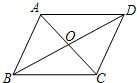 如图,四边形ABCD的对角线AC,BD交于O点,且AB$\stackrel{∥}{=}$CD,那么图中的全等三角形有( )
如图,四边形ABCD的对角线AC,BD交于O点,且AB$\stackrel{∥}{=}$CD,那么图中的全等三角形有( )
 如图,四边形ABCD的对角线AC,BD交于O点,且AB$\stackrel{∥}{=}$CD,那么图中的全等三角形有( )
如图,四边形ABCD的对角线AC,BD交于O点,且AB$\stackrel{∥}{=}$CD,那么图中的全等三角形有( )| A. | 2对 | B. | 3对 | C. | 4对 | D. | 5对 |
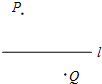 已知:如图,点P,点Q分别代表两个小区,直线l代表两个小区中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站点.
已知:如图,点P,点Q分别代表两个小区,直线l代表两个小区中间的一条公路.根据居民出行的需要,计划在公路l上的某处设置一个公交站点.