题目内容
9.如图1,△ABC与△ADE均是顶角为40°的等腰三角形,BC、DE分别是底边,求证:BD=CE.(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM
为△DCE中DE边上的高,连接BE.
①求∠AEB的度数;
②证明:AE=BE+2CM.
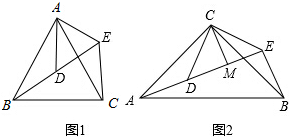
分析 (1)根据全等三角形的判定方法,判断出△BAD≌△CAE,即可判断出BD=CE.
(2)①首先根据△ACB和△DCE均为等腰直角三角形,可得AC=BC,CD=CE,∠ACB=∠DCE=90°,据此判断出∠ACD=∠BCE;然后根据全等三角形的判定方法,判断出△ACD≌△BCE,即可判断出BE=AD,∠BEC=∠ADC,进而判断出∠AEB的度数为90°即可;
②根据DCE=90°,CD=CE,CM⊥DE,可得CM=DM=EM,所以DE=DM+EM=2CM,据此判断出AE=BE+2CM即可.
解答 (1)证明:∵∠BAC=∠DAE=40°,
∴∠BAC-∠DAC=∠DAE-∠DAC,
即∠BAD=∠CAE,
在△BAD和△CAE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△BAD≌△CAE,
∴BD=CE.
(2)解:①∵△ACB和△DCE均为等腰直角三角形,
∴AC=BC,CD=CE,∠ACB=∠DCE=90°,∠CDE=∠CED=45°,
∴∠ACB-∠DCB=∠DCE-∠DCB,
即∠ACD=∠BCE,
在△ACD和△BCE中,
$\left\{\begin{array}{l}{AC=BC}\\{∠ACD=∠BCE}\\{CD=CE}\end{array}\right.$,
∴△ACD≌△BCE,
∴BE=AD,∠BEC=∠ADC,
∵点A,D,E在同一直线上,
∴∠ADC=180-45=135°,
∴∠BEC=135°,
∴∠AEB=∠BEC-∠CED=135-45=90°;
②∵∠DCE=90°,CD=CE,CM⊥DE,
∴CM=DM=EM,
∴DE=DM+EM=2CM,
∴AE=AD+DE=BE+2CM.
点评 此题主要考查了全等三角形的判定方法和性质,等腰直角三角形的性质和应用,要熟练掌握,解答此题的关键是要明确:在判定三角形全等时,关键是选择恰当的判定条件.

 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案| A. | 单项式5xyz的次数是1 | B. | 单项式-$\frac{ab}{3}$的系数是-3 | ||
| C. | 多项式x-4的常数项是4 | D. | 多项式a2b-2a5+b4是五次三项式 |
| A. | (-2)2-(-22) | B. | -22-22 | C. | -22+(-2)2 | D. | -22-(-2)2 |
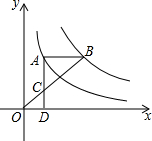 如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )
如图,点A在双曲线y=$\frac{3}{x}$上,点B在双曲线y=$\frac{k}{x}$(k≠0)上,AB∥x轴,过点A作AD⊥x轴于D.连接OB,与AD相交于点C,若AC=2CD,则k的值为( )| A. | 6 | B. | 9 | C. | 10 | D. | 12 |
| A. | 1,2,3 | B. | 6,8,12 | C. | 5,12,5 | D. | 7,24,25 |
 如图,数轴上A,B两点表示的数是互为相反数,且点A与点B之间的距离为4个单位长度,则点A表示的数是-2.
如图,数轴上A,B两点表示的数是互为相反数,且点A与点B之间的距离为4个单位长度,则点A表示的数是-2.