题目内容
某班同学去18千米的北山郊游.只有一辆汽车,需分两组,甲组先乘车、乙组步行.车行至A处,甲组下车步行,汽车返回接乙组,最后两组同时达到北山站.已知汽车速度是60千米/时,步行速度是4千米/时,求A点距北山站的距离.
考点:一元一次方程的应用
专题:
分析:设A点距离起点的距离为s,则:甲组到达A点所用的时间t1=
,那么,在这段时间内乙组前行的距离为
×4=
;最后两组同时到达终点,所以:
=
,求出S后,即能求出A点距离北山(终点)的距离为多少千米.
| s |
| 60 |
| s |
| 60 |
| s |
| 15 |
18-
| ||
|
18-
| ||
| 60 |
解答:解:设A点距离起点的距离为s,则:
甲组到达A点所用的时间t1=
,那么,在这段时间内乙组前行的距离为
×4=
;
那么,汽车返回去接乙组时,车于乙组之间的距离为s-
=
;
而这时汽车与乙组之间是相向运动,他们相遇需要的时间t2=
=
;
那么,在t2这段时间内,甲乙两组均向前前行的距离=4×
=
;
因此,甲组距离终点的距离=(18-s)-=
=18-
;
乙组(和车)距离终点的距离=18-
-
=18-
,
因为最后两组同时到达终点,所以:
=
,
270-
=18-
,
=152,
解得:s=16
18-16=2(千米)
答:A点距北山站相距2千米.
甲组到达A点所用的时间t1=
| s |
| 60 |
| s |
| 60 |
| s |
| 15 |
那么,汽车返回去接乙组时,车于乙组之间的距离为s-
| s |
| 15 |
| 14s |
| 15 |
而这时汽车与乙组之间是相向运动,他们相遇需要的时间t2=
| ||
| 60+4 |
| 7s |
| 15×32 |
那么,在t2这段时间内,甲乙两组均向前前行的距离=4×
| 7s |
| 15×32 |
| 7s |
| 120 |
因此,甲组距离终点的距离=(18-s)-=
| 7s |
| 120 |
| 127s |
| 120 |
乙组(和车)距离终点的距离=18-
| s |
| 15 |
| 7s |
| 120 |
| s |
| 8 |
因为最后两组同时到达终点,所以:
18-
| ||
|
18-
| ||
| 60 |
270-
| 127s |
| 8 |
| s |
| 8 |
| 126s |
| 8 |
解得:s=16
18-16=2(千米)
答:A点距北山站相距2千米.
点评:本题考查了行程问题的追击问题,相遇问题之间的数量关系的运用,列一元一次方程解实际问题的运用,解答时根据行程问题的数量关系建立方程是关键.

练习册系列答案
相关题目
 李明在小岛上的A处,上午8时测得在A的北偏东60°的D处有一艘轮船,9时20分测得该船航行到北偏西60°的C处,9时40分测得该船到达位于A正西方5千米的港口B处,如果该船始终保持匀速直线运动,求:
李明在小岛上的A处,上午8时测得在A的北偏东60°的D处有一艘轮船,9时20分测得该船航行到北偏西60°的C处,9时40分测得该船到达位于A正西方5千米的港口B处,如果该船始终保持匀速直线运动,求: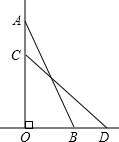 如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m,如果梯子的顶端A尚墙下滑0.5m,那么梯子底端B向外移了多少米?
如图,一架2.6m长的梯子AB斜靠在一竖直的墙AO上,这时AO为2.4m,如果梯子的顶端A尚墙下滑0.5m,那么梯子底端B向外移了多少米? 如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.
如图,在矩形ABCD中,E是BC边上的点,AE=BC,DF⊥AE,垂足为F,连接DE.