题目内容
你能比较两个数20102011和20112010的大小吗?为了解决这个问题,先把问题一般化,即比较nn+1和(n+1)n的大小(n≥1且n为整数):然后从分析n=1,n=2,n=3…这些简单的情形入手,从中发现规律,经过归纳、总结,最后猜想出结论.
(1)通过计算,比较下列各组数的大小(在横线处填上“>”、“=”或“<”):
①12 21;②23 32;③34 43;④45 54;
⑤56 65;⑥67 76;⑦78 87…
(2)由第(1)小题的结果归纳、猜想nn+1与(n+1)n的大小关系.
(3)根据第(2)小题得到的一般结论,可以得到20102011 20112010(填“>”、“=”或“<”).
(1)通过计算,比较下列各组数的大小(在横线处填上“>”、“=”或“<”):
①12
⑤56
(2)由第(1)小题的结果归纳、猜想nn+1与(n+1)n的大小关系.
(3)根据第(2)小题得到的一般结论,可以得到20102011
考点:幂的乘方与积的乘方
专题:阅读型,规律型
分析:(1)先通过计算比较(1)中的数据大小.
(2)从(1)中通过归纳可以得出nn+1与(n+1)n的大小关系是当n=1或n=2时,nn+1<(n+1)n;当n≥3时,n n+1>(n+1)n;
(3)直接利用(2)中结论得出(3)中的答案即可.
(2)从(1)中通过归纳可以得出nn+1与(n+1)n的大小关系是当n=1或n=2时,nn+1<(n+1)n;当n≥3时,n n+1>(n+1)n;
(3)直接利用(2)中结论得出(3)中的答案即可.
解答:解:(1)①12<21;②23<32;③34>43;④45>54;⑤56>6 5⑥67>76;⑦78>87;
故答案为:<,<,>,>,>,>,>;
(2)由(1)可知,当n=1、2时,nn+1<(n+1)n;当n≥3时,nn+1>(n+1)n;
(3)∵2010>3,2011>3,
∴20102011>20112010.
故答案为:>.
故答案为:<,<,>,>,>,>,>;
(2)由(1)可知,当n=1、2时,nn+1<(n+1)n;当n≥3时,nn+1>(n+1)n;
(3)∵2010>3,2011>3,
∴20102011>20112010.
故答案为:>.
点评:本题考查的是幂的乘方与积的乘方,解题关键是会从材料中找到数据之间的关系,并利用数据之间的规律总结出一般结论,然后利用结论直接进行解题.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
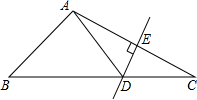 如图,在△ABC中,DE是AC的垂直平分线,AC=6cm,且△ABD的周长为13cm,则△ABC的周长为( )cm.
如图,在△ABC中,DE是AC的垂直平分线,AC=6cm,且△ABD的周长为13cm,则△ABC的周长为( )cm.| A、13 | B、19 | C、10 | D、16 |
 如图,有A、B、C、D 四张卡片,其正面分别写有“寸、又、日”四个偏旁部首,有的能独立成字,有的能组合成字.现四张卡片背面朝上.
如图,有A、B、C、D 四张卡片,其正面分别写有“寸、又、日”四个偏旁部首,有的能独立成字,有的能组合成字.现四张卡片背面朝上.