Question

16．已知，如图，四边形ABCD中，AB=AD，∠BAD=∠BCD=90°，E为BC边上一点，作∠AEF=∠ACF=90°
（1）试判断AE和EF的数量关系，并说明理由；
（2）当四边形ABCD的面积为16，BC的长为6，求AD的长．

Answer 1

分析 （1）作AM⊥BC，AN⊥CD垂足分别为M、N，在线段AM上截取AH=CE，连接HE，通过△AMB≌△AND证明四边形AMCN是正方形，然后再证明△AHE≌△ECF即可．
（2）先证明S_{四边形ABCD}=S_{正方形AMCN}=16，求出正方形边长，在RT△ADN中利用勾股定理即可解决．

解答 （1）解：作AM⊥BC，AN⊥CD垂足分别为M、N，在线段AM上截取AH=CE，连接HE．
∵∠AMC=∠MCN=∠=90°，
∴四边形AMCN是矩形，
∴∠MAN=90°，
∵∠BAD=90°，
∴∠BAD=∠MAN，
∴∠BAM=∠DAN，
在△AMB和△AND中，
$\left\{\begin{array}{l}{∠BAM=∠NAD}\\{∠AMB=∠N}\\{AB=AD}\end{array}\right.$，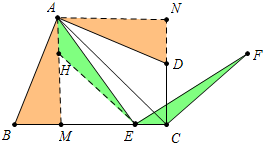
∴△AMB≌△AND，
∴AM=AN，
∴四边形AMCN是正方形，
∴AM=CM，∠ACM=45°，
∵∠ACF=90°，
∴∠ECF=135°，
∵AH=EC，
∴MH=ME，
∴∠MHE=45°，∠AHE=135°=∠ECF，
∵∠FEC+∠AEM=90°，∠HAE+∠AEM=90°，
∴∠FEC=∠HAE，
在△AHE和△ECF中，
$\left\{\begin{array}{l}{∠HAE=∠CEF}\\{AH=EC}\\{∠AHE=∠ECF}\end{array}\right.$，
∴△AHE≌△ECF，
∴AE=EF．
（2）由（1）可知：四边形AMCN是正方形，△AMB≌△AND，
∴S_△AMB=S_△AND，
∴S_{四边形ABCD}=S_{正方形AMCN}=16，
∴AN=MC=4，
∵BC=6，
∴MB=ND=2，
在RT△AND中，∵AN=4，ND=2，
∴AD=$\sqrt{A{N}^{2}+N{D}^{2}}$=$\sqrt{{4}^{2}+{2}^{2}}$=2$\sqrt{5}$．

点评 本题考查全等三角形的判定和性质、正方形的判定和性质、面积问题等知识，通过辅助线构造正方形是解决问题的关键．