题目内容
11.在Rt△ABC中,D为斜边AB的中点,E,F分别在AC,BC上,∠EDF=90°,已知CE=4,AE=2,BF-CF=$\frac{3}{2}$,求AB.分析 延长FD至点G,使得DG=DF,连接BG,EG,易证△ADG≌△BDF,可得AG=BF,∠DAG=∠B,可证明∠EAG=90°,根据等腰三角形底边三线合一性质可得EF=EG,设BF=AG=x,由勾股定理得出方程,解方程求出BF、CF,再由勾股定理求出AB即可即可.
解答 解:延长FD至点G,使得DG=DF,连接AG,EG,EF,如图所示:
∵D为斜边AB的中点,
∴AD=BD,
在△ADG和△BDF中,
$\left\{\begin{array}{l}{AD=BD}&{\;}\\{∠ADG=∠BDF}&{\;}\\{DG=DF}&{\;}\end{array}\right.$,
∴∴△ADG≌△BDF(SAS),
∴AG=BF,∠DAG=∠DBF,
∵∠DBF+∠BAC=90°,
∴∠DAG+∠BAC=90°,
即∠EAG=90°,
∴EG2=AG2+AE2,
设BF=AG=x,
∵BF-CF=$\frac{3}{2}$,
∴CF=x-$\frac{3}{2}$,
∵∠EDF=90°,
∴DE⊥FG,
∵DG=DF,
∴EF=EG,
∴EF2=EG2,
在Rt△CEF中,EF2=CE2+CF2,
∴AG2+AE2=CE2+CF2,
即x2+22=42+(x-$\frac{3}{2}$)2,
解得:x=$\frac{19}{4}$,
∴BF=$\frac{19}{4}$,CF=x-$\frac{3}{2}$=$\frac{13}{4}$,
∴BC=BF+CF=8,
∵∠C=90°,AC=AE+CE=6,
∴AB=$\sqrt{{8}^{2}+{6}^{2}}$=10.
点评 本题考查了全等三角形的判定与性质、勾股定理、线段垂直平分线的性质等知识;本题综合性强有一定难度,证明△ADG≌△BDF是解题的关键.

 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案 已知△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,AC=2$\sqrt{2}$,AD=1,F是BE的中点.若将△ADE绕点A旋转一周,则线段AF长度的取值范围是( )
已知△ABC和△ADE都是等腰直角三角形,∠ACB=∠ADE=90°,AC=2$\sqrt{2}$,AD=1,F是BE的中点.若将△ADE绕点A旋转一周,则线段AF长度的取值范围是( )| A. | $\frac{4-\sqrt{2}}{2}$≤AF≤$\frac{4+\sqrt{2}}{2}$ | B. | 2≤AF≤3 | C. | $\frac{4-\sqrt{2}}{2}$≤AF≤3 | D. | $\frac{2-\sqrt{2}}{2}$≤AF≤$\frac{2+\sqrt{2}}{2}$ |
 如图为等边三角形ABC与正方形DEFG的重叠情形,其中D,E两点分别在AB,BC上,且BD=BE.若AC=18,GF=6,则点F到AC的距离为( )
如图为等边三角形ABC与正方形DEFG的重叠情形,其中D,E两点分别在AB,BC上,且BD=BE.若AC=18,GF=6,则点F到AC的距离为( )| A. | 6$\sqrt{2}$-6 | B. | 6$\sqrt{3}$-6 | C. | 2$\sqrt{5}$ | D. | 3$\sqrt{3}$ |
 ,PD=10,则PE的长度为_____.
,PD=10,则PE的长度为_____.
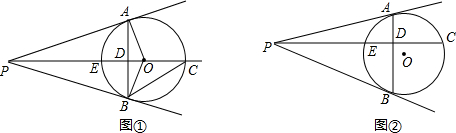
 已知,如图,四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,E为BC边上一点,作∠AEF=∠ACF=90°
已知,如图,四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,E为BC边上一点,作∠AEF=∠ACF=90°