题目内容
1. 若以△ABC两边AB、BC为边分别向外作等腰Rt△ABE和等腰Rt△BCH,连接AH、CE交于点O,过点B作BM⊥AC,垂足为M,延长MB交EH于N,求证:
若以△ABC两边AB、BC为边分别向外作等腰Rt△ABE和等腰Rt△BCH,连接AH、CE交于点O,过点B作BM⊥AC,垂足为M,延长MB交EH于N,求证:(1)AH=CE;
(2)AH⊥CE;
(3)EN=HN.
分析 (1)根据等腰直角三角形的性质得到AB=BE,BC=BH,∠ABE=∠CBH=90°,求得∠ABH=∠EBC,推出△ABH≌△EBC,根据全等三角形的性质得到结论;
(2)根据全等三角形的性质得到∠BAH=∠CEB,推出A,G,B,E四点共圆,根据圆周角定理得到∠AGE=∠ABE=90°,即可得到结论;
(3)过E作EF⊥MN于F,HQ⊥MN于Q,根据余角的性质得到∠HBQ=∠BCM,推出△BHQ≌△BMC,根据全等三角形的性质得到HQ=BM,同理EF=BM,等量代换得到EF=HQ,推出△EFN≌△HQN,根据全等三角形的性质即可得到结论.
解答 证明:(1)∵△ABE与△BCH是等腰直角三角形,
∴AB=BE,BC=BH,∠ABE=∠CBH=90°,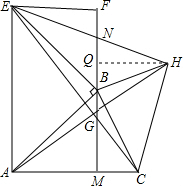
∴∠ABH=∠EBC,
在△ABH与△EBC中,$\left\{\begin{array}{l}{AB=BE}\\{∠ABH=∠EBC}\\{BH=BC}\end{array}\right.$,
∴△ABH≌△EBC,
∴AH=CE;
(2)∵△ABH≌△EBC,
∴∠BAH=∠CEB,
∴A,G,B,E四点共圆,
∴∠AGE=∠ABE=90°,
∴AH⊥CE;
(3)过E作EF⊥MN于F,HQ⊥MN于Q,
∵∠HBQ+∠MBC=90°,∠BCM+∠MBC=90°,
∴∠HBQ=∠BCM,
在△BHQ与△BMC中,$\left\{\begin{array}{l}{∠HBQ=∠BCM}\\{∠HQB=∠BMC=90°}\\{BH=BC}\end{array}\right.$,
∴△BHQ≌△BMC,
∴HQ=BM,同理EF=BM,
∴EF=HQ,
在△EFN与△HQN中,$\left\{\begin{array}{l}{∠F=∠HQN=90°}\\{EF=HQ}\\{∠ENF=∠HNQ}\end{array}\right.$,
∴△EFN≌△HQN,
∴EN=HN.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,四点共圆,熟练掌握全等三角形的判定和性质是解题的关键.

| A. | 有理数中,没有最大和最小的数 | |
| B. | 零是最小的有理数 | |
| C. | π四舍五入精确到0.1约等于3.1 | |
| D. | “小王身高1.60米”中的“1.60”是近似数 |
 B.
B.  C.
C.  D.
D. 
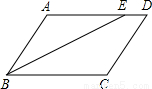
 如图,已知AB∥CD,AE∥CF,DE=BF,试说明:
如图,已知AB∥CD,AE∥CF,DE=BF,试说明: 已知,如图,四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,E为BC边上一点,作∠AEF=∠ACF=90°
已知,如图,四边形ABCD中,AB=AD,∠BAD=∠BCD=90°,E为BC边上一点,作∠AEF=∠ACF=90°