��Ŀ����
5�� ��ͼ����֪������y=k��x+2����x-4����kΪ��������k��0����x��Ľ���ΪA��B����y��Ľ���ΪC��������B��ֱ��y=-$\frac{1}{2}$x+b�������ߵ���һ������ΪD��
��ͼ����֪������y=k��x+2����x-4����kΪ��������k��0����x��Ľ���ΪA��B����y��Ľ���ΪC��������B��ֱ��y=-$\frac{1}{2}$x+b�������ߵ���һ������ΪD����1������D�ĺ�����Ϊx=-4�������һ�κ����������ߵĽ���ʽ��
��2����ֱ��mƽ���ڸ������ߵĶԳ��ᣬ���ҿ������߶�AB�������ƶ�������ֱ��BD�������߷ֱ��ڵ�E��F����m�ƶ���ʲôλ��ʱ��EF��ֵ������ֵ�Ƕ��٣�
��3����ԭ�������ڵ�һ�����Ƿ���ڵ�F��ʹ�á�APB�ס�ABC�������ڣ���ֱ��д����ʱk��ֵ���������ڣ���˵�����ɣ�
���� ��1���Ƚⷽ��k��x+2����x-4��=0�ɵ�A��-2��0����B��4��0�����ٰ�B���������y=-$\frac{1}{2}$x+b�������b=2����ɵõ�һ�κ�������ʽΪy=-$\frac{1}{2}$x+2����������һ�κ�������ʽȷ��D�����꣬Ȼ���D������������y=k��x+2����x-4�������k��ֵ���ɵõ��������߽���ʽ��
��2�����ö��κ�����һ�κ���ͼ���ϵ����������������F��t��$\frac{1}{4}$t2-$\frac{1}{2}$t-2������E��t��-$\frac{1}{2}$t+2����-2��t��4�����ǵõ�EF=-$\frac{1}{2}$t+2-��$\frac{1}{4}$t2-$\frac{1}{2}$t-2��=-$\frac{1}{4}$t2+4��Ȼ����ݶ��κ�����������⣻
��3����PH��x����H����ͼ���ȱ�ʾ��C������Ϊ��0��-8k������P[n��k��n+2����n-4��]���������������ε��ж�����������PAB=��CAB��AP��AB=AB��ACʱ����APB�ס�ABC���ٸ������ж��壬��Rt��APH����tan��PAH=$\frac{k��n+2����n-4��}{n+2}$����Rt��OAC����tan��OAC=$\frac{8k}{2}$=4k����$\frac{k��n+2����n-4��}{n+2}$=4k�����n=8�����ǵõ�P��8��40k�����������ù��ɶ��������AP=10$\sqrt{16{k}^{2}+1}$��AC=2$\sqrt{16{k}^{2}+1}$��Ȼ������AP��AB=AB��AC�õ�10$\sqrt{16{k}^{2}+1}$•2$\sqrt{16{k}^{2}+1}$=62�����k1=$\frac{\sqrt{5}}{10}$��k2=-$\frac{\sqrt{5}}{10}$����ȥ�������ǿ�ȷ��P�����꣮
���  �⣺��1����y=0ʱ��k��x+2����x-4��=0�����x1=-2��x2=4����A��-2��0����B��4��0����
�⣺��1����y=0ʱ��k��x+2����x-4��=0�����x1=-2��x2=4����A��-2��0����B��4��0����
��B��4��0������y=-$\frac{1}{2}$x+b��-2+b=0�����b=2��
����һ�κ�������ʽΪy=-$\frac{1}{2}$x+2��
��x=-4ʱ��y=-$\frac{1}{2}$x+2=4����D������Ϊ��4��4����
��D��-4��4������y=k��x+2����x-4����k•��-2��•��-8��=4�����k=$\frac{1}{4}$��
���������߽���ʽΪy=$\frac{1}{4}$��x+2����x-4������y=$\frac{1}{4}$x2-$\frac{1}{2}$x-2��
��2����F��t��$\frac{1}{4}$t2-$\frac{1}{2}$t-2������E��t��-$\frac{1}{2}$t+2����-2��t��4��
����EF=-$\frac{1}{2}$t+2-��$\frac{1}{4}$t2-$\frac{1}{2}$t-2��=-$\frac{1}{4}$t2+4��
���Ե�t=0ʱ��EF������ֵΪ4��
����ֱ��m�ƶ�����y���غϵ�λ��ʱ��EF��ֵ������ֵ��4��
��3�����ڣ�
��PH��x����H����ͼ��
��x=0ʱ��y=k��x+2����x-4��=-8k����C��0��-8k����
��P[n��k��n+2����n-4��]��
����PAB=��CAB��AP��AB=AB��ACʱ����APB�ס�ABC��
��Rt��APH��tan��PAH=$\frac{k��n+2����n-4��}{n+2}$��
��Rt��OAC��tan��OAC=$\frac{8k}{2}$=4k��
��$\frac{k��n+2����n-4��}{n+2}$=4k�����n=8����P��8��40k����
��AP=$\sqrt{P{H}^{2}+A{H}^{2}}$=$\sqrt{��40k��^{2}+1{0}^{2}}$=10$\sqrt{16{k}^{2}+1}$��
��AC=$\sqrt{O{C}^{2}+O{A}^{2}}$=$\sqrt{��8k��^{2}+{2}^{2}}$=2$\sqrt{16{k}^{2}+1}$��
��AP��AB=AB��AC��
��AP•AC=AB2��
��10$\sqrt{16{k}^{2}+1}$•2$\sqrt{16{k}^{2}+1}$=62��
��5��16k2+1��=9�����k1=$\frac{\sqrt{5}}{10}$��k2=-$\frac{\sqrt{5}}{10}$����ȥ����
��k=4$\sqrt{5}$��P��������8��4$\sqrt{5}$����
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ�����������Ͷ��κ��������ʣ����Ӧ�����ƱȺ��ɶ���������Ӧ�߶εij�������������ͼ�����ʣ�

 ��֪��ABC�͡�ADE���ǵ���ֱ�������Σ���ACB=��ADE=90�㣬AC=2$\sqrt{2}$��AD=1��F��BE���е㣮������ADE�Ƶ�A��תһ�ܣ����߶�AF���ȵ�ȡֵ��Χ�ǣ�������
��֪��ABC�͡�ADE���ǵ���ֱ�������Σ���ACB=��ADE=90�㣬AC=2$\sqrt{2}$��AD=1��F��BE���е㣮������ADE�Ƶ�A��תһ�ܣ����߶�AF���ȵ�ȡֵ��Χ�ǣ�������| A�� | $\frac{4-\sqrt{2}}{2}$��AF��$\frac{4+\sqrt{2}}{2}$ | B�� | 2��AF��3 | C�� | $\frac{4-\sqrt{2}}{2}$��AF��3 | D�� | $\frac{2-\sqrt{2}}{2}$��AF��$\frac{2+\sqrt{2}}{2}$ |
| A�� | �������У�û��������С���� | |
| B�� | �������������� | |
| C�� | ���������뾫ȷ��0.1Լ����3.1 | |
| D�� | ��С������1.60�ס��еġ�1.60���ǽ����� |
| A�� | 9 | B�� | 7 | C�� | 18 | D�� | 12 |
 .
. ����A��ֵ.
����A��ֵ. ��ʵ����Χ�������壬��x��ȡֵ��Χ�ǣ�������
��ʵ����Χ�������壬��x��ȡֵ��Χ�ǣ�������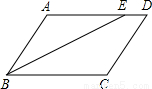
 ��ͼ����֪AB��CD��AE��CF��DE=BF����˵����
��ͼ����֪AB��CD��AE��CF��DE=BF����˵���� ��֪����ͼ���ı���ABCD�У�AB=AD����BAD=��BCD=90�㣬EΪBC����һ�㣬����AEF=��ACF=90��
��֪����ͼ���ı���ABCD�У�AB=AD����BAD=��BCD=90�㣬EΪBC����һ�㣬����AEF=��ACF=90��