题目内容
已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如表:
则当x≥1时,y的最小值是 .
| x | … | -1 | 0 | 1 | 4 | … |
| y | … | 10 | 5 | 2 | 5 | … |
考点:二次函数的最值
专题:
分析:先用待定系数法求出二次函数的解析式,得出其对称轴的直线方程,进而可得出结论.
解答:解:∵由表可知,当x=-1时,y=10,当x=0时,y=5,当x=1时,y=2,
∴
,解得
,
∴抛物线的解析式为y=x2-4x+5,
∴其对称轴为直线x=-
=-
=2.
∵x≥1,
∴当x=2时,y最小=
=
=1.
故答案为:1.
∴
|
|
∴抛物线的解析式为y=x2-4x+5,
∴其对称轴为直线x=-
| b |
| 2a |
| -4 |
| 2 |
∵x≥1,
∴当x=2时,y最小=
| 4ac-b2 |
| 4a |
| 20-16 |
| 4 |
故答案为:1.
点评:本题考查的是二次函数的最值,熟知用待定系数法求二次函数的解析式是解答此题的关键.

练习册系列答案
相关题目
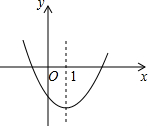 二次函数y=ax2+bx+c图象如图,下列正确的个数为( )
二次函数y=ax2+bx+c图象如图,下列正确的个数为( )①abc>0;②2a-3c<0;③2a+b>0;④ax2+bx+c=0有两个实数解x1,x2,且x1+x2<0; ⑤9a+3b+c>0;⑥当x<1时,y随x增大而减小.
| A、2 | B、3 | C、4 | D、5 |
 已知有理数a,b在数轴上表示的点如图所示,则下列式子中不正确的是( )
已知有理数a,b在数轴上表示的点如图所示,则下列式子中不正确的是( )| A、a•b<0 |
| B、a+b<0 |
| C、|a|<|b| |
| D、b-a>0 |
已知sinα<0.5,那么锐角α的取值范围是( )
| A、60°<α<90° |
| B、30°<α<90° |
| C、0°<α<60° |
| D、0°<α<30° |
 如图,梯形ABCD沿上底AD方向向右平移到梯形EFGH,AD=4,BC=8,若阴影部分面积是四边形ABGH的
如图,梯形ABCD沿上底AD方向向右平移到梯形EFGH,AD=4,BC=8,若阴影部分面积是四边形ABGH的 如图,将直线y=x沿x轴负方向平移4个单位后,恰好与双曲线y=
如图,将直线y=x沿x轴负方向平移4个单位后,恰好与双曲线y= 如图,要使△AFE∽△ABC,需要添加一个条件,请添加条件并给出证明过程.
如图,要使△AFE∽△ABC,需要添加一个条件,请添加条件并给出证明过程.