题目内容
20.若x2(x+1)+y(xy+y)=(x+1)•B(其中x≠-1),则B=x2+y2.分析 首先将y(xy+y)括号内提取公因式y,再通过移项、提取公因式x+1,将原式转化为(x+1)(x2+y2-B)=0.再根据已知x≠-1,故只能是x2+y2-B=0,至此问题得解.
解答 解:∵x2(x+1)+y(xy+y)=(x+1)•B,
⇒x2(x+1)+y2(x+1)-(x+1)•B=0,
⇒(x+1)(x2+y2-B)=0,
∵x≠-1,
∴x2+y2-B=0,即x2+y2=B.
故答案为:x2+y2.
点评 本题考查因式分解的应用.解决本题主要通过提取公因式(x+1)分解因式来实现.

练习册系列答案
相关题目
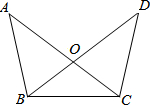 如图,已知∠ABO=∠DCO,OB=OC,求证:△ABC≌△DCB.
如图,已知∠ABO=∠DCO,OB=OC,求证:△ABC≌△DCB.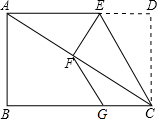 如图,已知点E是矩形一边AD上的一点,沿CE折叠矩形使点D落在对角线AC上的点F处,点G为BC上一点,且CG=DE,连FG.
如图,已知点E是矩形一边AD上的一点,沿CE折叠矩形使点D落在对角线AC上的点F处,点G为BC上一点,且CG=DE,连FG.
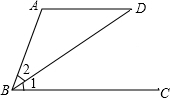 如图,已知AD∥BC,∠A:∠ABC=2:1,∠1=∠2,求∠ADB的度数.
如图,已知AD∥BC,∠A:∠ABC=2:1,∠1=∠2,求∠ADB的度数.