题目内容
19.若a、b、c是△ABC的三边,且a、b、c满足关系式|a-3|+(b-4)2=0,c是不等式组$\left\{\begin{array}{l}{\frac{x-3}{3}>x-4}\\{2x+3<\frac{6x+1}{2}}\end{array}\right.$的最大整数解,求△ABC的周长.分析 先根据题意,求出a和b的值,再求出不等式组中每个不等式的解集,然后求出其公共解集,最后求其整数解即可.
解答 解:∵a、b满足关系式|a-3|+(b-4)2=0,
∴a=3,b=4,
∵不等式组$\left\{\begin{array}{l}{\frac{x-3}{3}>x-4}\\{2x+3<\frac{6x+1}{2}}\end{array}\right.$的解集是:2.5<x<4.5,
∴最大整数解是4,∴c=4,
故△ABC三边的长分别为,3,4,4,
△ABC的周长为:3+4+4=11.
点评 本题考查不等式组的解法及整数解的确定.求不等式组的解集,应遵循以下原则:同大取较大,同小取较小,小大大小中间找,大大小小解不了.

练习册系列答案
 全能闯关100分系列答案
全能闯关100分系列答案
相关题目
10.(3a2-2a+2)-(a2-3a-4)=( )
| A. | a2+5a+6 | B. | -2a2+5a+6 | C. | 2a2-5a+6 | D. | 2a2+a+6 |
14.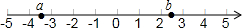 a、b在数轴上的位置如图,则下列结论正确的是( )
a、b在数轴上的位置如图,则下列结论正确的是( )
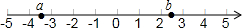 a、b在数轴上的位置如图,则下列结论正确的是( )
a、b在数轴上的位置如图,则下列结论正确的是( )| A. | a-b<0 | B. | ab>0 | C. | -a<b | D. | |a|<|b| |
11.目前,我国大约有1.3亿高血压病患者,预防高血压不容忽视.“千帕kpa”和“毫米汞柱mmHg”都是表示血压的单位.请你根据表格提供的信息,判断下列各组换算正确的是( )
| 千帕kpa | … | 10 | 12 | 14 | … |
| 毫米汞柱mmHg | … | 75 | 90 | 105 | … |
| A. | 6kpa=50mmHg | B. | 16kpa=110mmHg | C. | 20kpa=150mmHg | D. | 22kpa=160mmHg |
9.“每天锻炼一小时,健康生活一辈子”.新泰市自开展“阳光体育运动”以来,学校师生的锻炼意识都增强了,某校有学生3000人,为了解学生每天的锻炼时间,学校体育组随机调查了部分学生,统计结果如表所示.
该校每天锻炼时间达到1小时及以上的约有300人.
| 时间段 | 29分钟及以下 | 30-39分钟 | 40-49分钟 | 50-59分钟 | 1小时及以上 |
| 频数/人 | 108 | 20 | |||
| 频率 | 0.54 | 0.12 | 0.09 |