题目内容
8. 如图,在等边三角形ABC中,点M是BC边上的任意一点(不与端点重合),连接AM,以AM为边作等边三角形AMN,连接CN.
如图,在等边三角形ABC中,点M是BC边上的任意一点(不与端点重合),连接AM,以AM为边作等边三角形AMN,连接CN.(1)求∠ACN的度数.
(2)若点M在△ABC的边BC的延长线上,其他条件不变,则∠ACN的度数是否发生变化?(直接写出结论即可)
分析 (1)根据等边三角形的性质可得AB=AC,AM=AN,∠BAC=∠MAN=60°,进而得到∠BAM=∠CAN,再利用SAS可证明△BAM≌△CAN,继而得出结论;
(2)也可以通过证明△BAM≌△CAN,得出结论,和(1)的思路完全一样.
解答 (1)证明:∵△ABC、△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,∠B=60°,
∴∠BAM=∠CAN,
在△BAM和△CAN中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAM=∠CAN}\\{AM=AN}\end{array}\right.$,
∴△BAM≌△CAN(SAS),
∴∠ACN=∠B=60°;
(2)解:结论∠ACN=60°仍成立.如图,
理由如下:∵△ABC、△AMN是等边三角形,
∴AB=AC,AM=AN,∠BAC=∠MAN=60°,
∴∠BAM=∠CAN,
在△BAM和△CAN中,$\left\{\begin{array}{l}{AB=AC}\\{∠BAM=∠CAN}\\{AM=AN}\end{array}\right.$,
∴△BAM≌△CAN(SAS),
∴∠ACN=∠B=60°.
点评 本题主要考查了等边三角形的性质,以及全等三角形的判定与性质,解答本题的关键是仔细观察图形,找到全等的条件,利用全等的性质证明结论.

练习册系列答案
相关题目
16.已知x+y=-4,xy=2,则x2+y2的值( )
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
20.计算4x3•x2的结果是( )
| A. | 4x6 | B. | 4x5 | C. | 4x4 | D. | 4x3 |
18.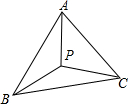 如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )
如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )
 如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )
如图,已知△APB和△APC是以AP所在的直线为对称轴的轴对称图形,若PA=PB,∠PAB=30°,则∠BPC的大小是( )| A. | 110° | B. | 130° | C. | 120° | D. | 140° |

 己知,如图,在△ABC中,∠C=90°,∠A=24°,请用直尺和圆规找到一条直线,把△ABC恰好分割成两个等腰三角形(不写作法,但需保留作图痕迹),直线CD即为所求.
己知,如图,在△ABC中,∠C=90°,∠A=24°,请用直尺和圆规找到一条直线,把△ABC恰好分割成两个等腰三角形(不写作法,但需保留作图痕迹),直线CD即为所求.