题目内容
10.解一元二次方程:①2x2-32=0
②x2-2$\sqrt{5}$x+1=0
③x(x-5)=2(x-5)
④(x-1)2-5(x-1)+6=0.
分析 ①方程整理后,利用平方根定义开方即可求出解.
②利用十字相乘法对等式的左边进行因式分解.
③先移项,然后利用提取公因式(x-5)对等式的左边进行因式分解.
④设t=x-1,则原方程转化为关于t的方程,通过解新方程求得t的值后再来求x的值.
解答 解:①方程整理得:x2=16,
开方得:x1=4,x2=-4.
②由原方程,得
(x-$\sqrt{5}$-2)(x-$\sqrt{5}$+2)=0,
解得 x1=$\sqrt{5}$+2,x2=$\sqrt{5}$-2.
③x(x-5)=2(x-5)
(x-2)(x-5)=0,
则x-2=0或x-5=0,
解得x1=2,x2=5.
④设t=x-1,则由原方程得到:t2-5t+6=0,
即(t-2)(t-3)=0,
解得t=2或t=3,
所以x-1=2或x-1=3,
解得x1=3,x2=4.
点评 本题考查了解一元二次方程的方法,需要根据方程的特点选择解答法方法.

练习册系列答案
 步步高口算题卡系列答案
步步高口算题卡系列答案 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
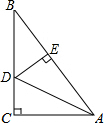 如图,△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,CD=2cm,DE⊥AB于E,则BD=( )
如图,△ABC中,∠C=90°,∠B=30°,AD平分∠BAC,CD=2cm,DE⊥AB于E,则BD=( )