题目内容

20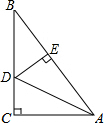．如图，△ABC中，∠C=90°，∠B=30°，AD平分∠BAC，CD=2cm，DE⊥AB于E，则BD=（　　）
A．1B．2C．3D．4

分析 根据角平分线性质求出CD的长和∠DAE的度数，根据含30度角的直角三角形性质求出BD即可．

解答 解：∵AD平分∠CAB，∠C=90°，DE⊥AB，
∴CD=DE=2cm，
∵∠B=30°，
∴BD=2DE=4cm，
故选：D．

点评 本题考查了对含30度角的直角三角形的性质和角平分线性质的应用，求出DE的长是解此题的关键．

练习册系列答案
相关题目
10．解一元二次方程：
①2x2-32=0  
②x2-2$\sqrt{5}$x+1=0   
③x（x-5）=2（x-5）
④（x-1）2-5（x-1）+6=0．
11．计算：
（1）5x-y+（6x-9y）
（2）（ab-3ab2）-（$\frac{1}{2}$ab+7ab2）
8．下列计算正确的是（　　）
A．$\sqrt{20}$=2$\sqrt{10}$B．$\sqrt{（-3）^{2}}$=-3C．$\sqrt{4}$-$\sqrt{2}$=$\sqrt{2}$D．$\sqrt{2}$•$\sqrt{3}$=$\sqrt{6}$
15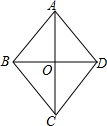．如图，在菱形ABCD中，AC与BD相交于点O，AO=4，BO=3，则菱形的边长AB等于（　　）
A．10B．$\sqrt{7}$C．6D．5
5．如图①，△ABC是边长为6cm的等边三角形，点M，N分别从点A，B同时出发，沿边AB，BC运动，且它们的速度都为1cm/s．设点M的运动时间为t （s）．
（1）在图①中，画出点M、N并连接MN，当t=2或4时，△BMN是直角三角形；
（2）如图②，连接AN、CM，相交于点P，当t=3时，△ABN≌△CBM；
（3）图②中，点M，N在运动的过程中，∠CPN的度数会发生变化吗？若变化，则说明理由；若不变，请求出它的度数．
12．以下列各组线段为边，能组成三角形的是（　　）
A．1，2，3B．3，3，6C．5，8，2D．4，5，6
9．计算6m2-5m+3与5m2+2m-1的差，结果是（　　）
A．m2-3m+4B．m2-3m+2C．m2-7m+2D．m2-7m+4
10．在下列各数中是无理数的有（　　）
$-\sqrt{（-5）^{2}}$、$\sqrt{36}$、$\frac{1}{7}$、0、-π、$\root{3}{11}$、3.1415、$\sqrt{\frac{1}{5}}$、2.010101…（相邻两个1之间有1个0）．
A．1个B．2个C．3个D．4个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网