题目内容
1.直线l经过第一、三、四象限,l的解析式是y=(m+2)x+n.则n的取值范围在数轴上表示为( )| A. |  | B. |  | C. |  | D. |  |
分析 根据一次函数图象与系数的关系得到m+2>0且n<0,解得m>-2,然后根据数轴表示不等式的方法进行判断.
解答 解:∵直线y=(m+2)x+n经过第一、三、四象限,
∴m+2>0且n<0,
故选:B.
点评 本题考查了一次函数图象与系数的关系:一次函数y=kx+b(k、b为常数,k≠0)是一条直线,当k>0,图象经过第一、三象限,y随x的增大而增大;当k<0,图象经过第二、四象限,y随x的增大而减小;图象与y轴的交点坐标为(0,b).也考查了在数轴上表示不等式的解集.

练习册系列答案
相关题目
11. 如图,已知△ACD∽△BCA,若CD=4,AC=6,则BC等于( )
如图,已知△ACD∽△BCA,若CD=4,AC=6,则BC等于( )
 如图,已知△ACD∽△BCA,若CD=4,AC=6,则BC等于( )
如图,已知△ACD∽△BCA,若CD=4,AC=6,则BC等于( )| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
9.己知方程x2-7x+12=0的两根恰好是一个直角三角形的两条直角边的长,则这个直角三角形的斜边上的高为( )
| A. | 12 | B. | 6 | C. | 5 | D. | $\frac{12}{5}$ |
6.某公司生产的一种时令商品每件成本为20元,经过市场调研发现,这种商品在未来20天内的日销售量m(件)与时间t(天)的关系如表:
未来20天内每天的价格y(元/件)与时间t(天)的函数关系式为y=$\frac{1}{4}$t+25(1≤t≤20且t为整数).
(1)认真分析表中的数据,用所学过的函数知识,确定一个满足这些数据的m(件)与t(天)之间的关系式;
(2)设未来20天日销售利润为p(元).请求出p(元)与t(天)之间的关系式;并预测未来20天中哪一天的日销售利润最大,最大日销售利润是多少?
| 时间t(天) | 1 | 3 | 6 | 10 | … |
| 日销售量m(件) | 94 | 90 | 84 | 76 | … |
(1)认真分析表中的数据,用所学过的函数知识,确定一个满足这些数据的m(件)与t(天)之间的关系式;
(2)设未来20天日销售利润为p(元).请求出p(元)与t(天)之间的关系式;并预测未来20天中哪一天的日销售利润最大,最大日销售利润是多少?
13.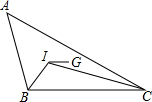 如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )
如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )
 如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )
如图,在△ABC中,G是重心,I是∠B和∠C的平分线的交点,若IG∥BC,且BC=5,则AB+BC等于( )| A. | 8 | B. | 10 | C. | 12 | D. | 14 |
10.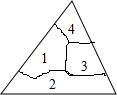 小明不慎将一个三角形玻璃摔碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是( )
小明不慎将一个三角形玻璃摔碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是( )
 小明不慎将一个三角形玻璃摔碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是( )
小明不慎将一个三角形玻璃摔碎成如图所示的四块,现要到玻璃店配一个与原来一样大小的三角形玻璃,你认为应带去的一块是( )| A. | 第1块 | B. | 第2块 | C. | 第3块 | D. | 第4块 |
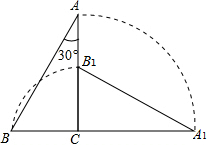 如图,把一个斜边长为4且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的面积是$\frac{11}{3}$π+$\sqrt{3}$.
如图,把一个斜边长为4且含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到△A1B1C,则在旋转过程中这个三角板扫过的面积是$\frac{11}{3}$π+$\sqrt{3}$. 如图,截去正方形ABCD的∠A,∠C后,∠1,2,∠3,∠4的和为540°.
如图,截去正方形ABCD的∠A,∠C后,∠1,2,∠3,∠4的和为540°.